
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
(1)判断直线AC与△DBE外接圆的位置关系,并说明理由;
(2)若AD=6,AE=6![]() ,求BC的长.
,求BC的长.
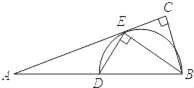
【答案】(1)直线AC与△DBE外接圆相切.(2)BC=4.
【解析】
(1)取BD的中点O,连接OE,证明∠OEB=∠CBE后可得OE⊥AC;
(2)设OD=OE=OB=x,利用勾股定理求出x的值,再证明△AOE∽△ABC,利用线段比求解.
(1)直线AC与△DBE外接圆相切.
理由:∵DE⊥BE
∴BD为△DBE外接圆的直径
取BD的中点O(即△DBE外接圆的圆心),连接OE
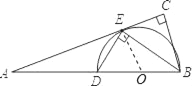
∴OE=OB
∴∠OEB=∠OBE
∵BE平分∠ABC
∴∠OBE=∠CBE
∴∠OEB=∠CBE
∵∠CBE+∠CEB=90°
∴∠OEB+∠CEB=90°,即OE⊥AC
∴直线AC与△DBE外接圆相切;
(2)设OD=OE=OB=x
∵OE⊥AC
∴(x+6)2﹣(6![]() )2=x2
)2=x2
∴x=3
∴AB=AD+OD+OB=12
∵OE⊥AC
∴△AOE∽△ABC
∴![]() ,即
,即![]()
∴BC=4.


科目:初中数学 来源: 题型:
【题目】如图,已知⊙C的半径为2,圆外一点O满足OC=3.5,点P为⊙C上一动点,经过点O的直线l上有两点A、B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值为( )
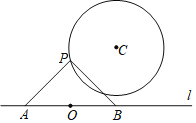
A. 2 B. 2.5 C. 3 D. 3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两城市相距100km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区.为什么?(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
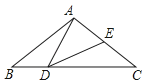
【题目】如图,在△ABC中,点D是边BC上的一点,点E是边AC上的一点,且AB=AC=DC,BD=CE,连接AD、DE.
(1)求证:△ADE是等腰三角形;
(2)若∠ADE=40°,请求出∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,求大树CD的高度?(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
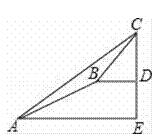
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE.
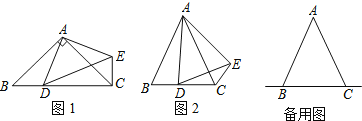
(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE= °.
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由.
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店打出促销广告:最潮新款服装30件,每件售价300元.若一次性购买不超过10件时,售价不变;若一次性购买超过10件时,每多买1件,所买的每件服装的售价均降低3元.已知该服装成本是每件200元,设顾客一次性购买服装x件时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少件时,该网店从中获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4的等边三角形,点D是AB上异于A,B的一动点,将△ACD绕点C逆时针旋转60°得△BCE,则旋转过程中△BDE周长的最小值_____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com