
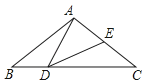
【题目】如图,在△ABC中,点D是边BC上的一点,点E是边AC上的一点,且AB=AC=DC,BD=CE,连接AD、DE.
(1)求证:△ADE是等腰三角形;
(2)若∠ADE=40°,请求出∠BAC的度数.
【答案】(1)证明见解析;(2)100°.
【解析】
(1)由“SAS”可证△ABD≌△DCE,可得AD=AE,即△ADE是等腰三角形;
(2)由全等三角形的性质可得∠BAD=∠EDC,由三角形内角和定理可求解.
证明:(1)∵AB=AC,
∴∠B=∠C,
在△ABD和△DCE中.
 ,
,
∴△ABD≌△DCE(SAS),
∴AD=DE,
∴△ADE是等腰三角形;
(2)∵△ABD≌△DCE,
∴∠BAD=∠EDC,
∴∠BAD+∠BDA=∠BDA+∠EDC=180°﹣∠ADE=140°,
∴在△ABD中,∠B=180°﹣140°=40°,
∴∠C=∠B=40°,
∴∠BAC=180°﹣40°﹣40°=100°.


科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD和AEFG是两个互相重合的矩形,如图2将矩形AEFG绕点A按顺时针方向旋转α度(0≤α≤90°),点G恰好落在矩形ABCD的对角线上,AB与FG相交于点M,连接BE交FG于点N.
(1)当AB=AD时,请直接写出∠ABE的度数;
(2)当∠ADB=60°时,求∠ABE的度数;
(3)如图3,当AB=2AD=2时,①求点A到直线BE的距离; ②直接写出△BMN的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
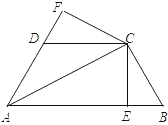
(1)求证:△BCE≌△DCF;
(2)若AB=21,AD=9,BC=CD=10,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
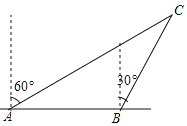
【题目】如图,某渔船向正东方向以12海里/时的速度航行,在A处测得岛C在北偏东的60°方向,1小时后渔船航行到B处,测得岛C在北偏东的30°方向,已知该岛周围10海里内有暗礁.
(1)B处离岛C有多远?
(2)如果渔船继续向东航行,有无触礁危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是随机抽取的某公司部分员工的月收入资料.
月收入/元 | 45000 | 18000 | 10000 | 5500 | 5000 | 3400 | 3000 | 2000 |
人数 | 1 | 1 | 1 | 3 | 6 | 1 | 11 | 2 |
(1)请计算样本的平均数和中位数;
(2)甲乙两人分别用样本平均数和中位数来估计推断公司全体员工月收入水平,请你写出甲乙两人的推断结论;并指出谁的推断比较科学合理,能直实地反映公司全体员工月收入水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
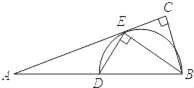
【题目】如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB边上且DE⊥BE.
(1)判断直线AC与△DBE外接圆的位置关系,并说明理由;
(2)若AD=6,AE=6![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究新知:

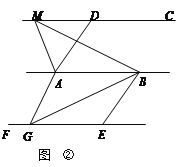
①如图,已知AD∥BC,AD=BC,点M,N是直线CD上任意两点.试判断△ABM与△ABN的面积是否相等.
②如图,已知AD∥BE,AD=BE,AB∥CD∥EF,点M是直线CD上任一点,点G是直线EF上任一点.试判断△ABM与△ABG的面积是否相等,并说明理由.
(2)结论应用:
如图③,抛物线![]() 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线![]() 上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?若存在,请求出此时点E的坐标,若不存在,请说明理由.
上是否存在除点C以外的点E,使得△ADE与△ACD的面积相等?若存在,请求出此时点E的坐标,若不存在,请说明理由.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com