
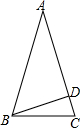
 如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )
如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD=( )| A. | 36° | B. | 54° | C. | 18° | D. | 64° |
科目:初中数学 来源: 题型:解答题
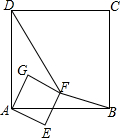 正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )
如图,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=$\frac{72}{5}$.在以上4个结论中,正确的有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
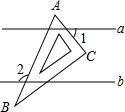 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
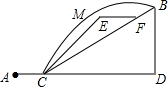 如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )
如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )| A. | A→C→D→B | B. | A→C→F→B | C. | A→C→E→F→B | D. | A→C→M→B |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
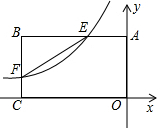 如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(-1,2).
如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(-1,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com