
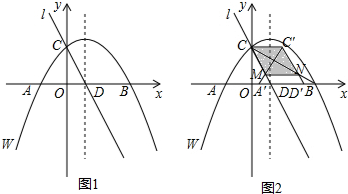
分析 (1)根据自变量与函数值对应关系,当函数值为零时,可得A、B点坐标,当自变量为零时,可得C点坐标,根据对称轴公式,可得D点坐标,根据待定系数法,可得l的解析式;
(2)根据余角性质,可得∠1与∠3的关系,根据正切的定义,可得关于F点的横坐标的方程,根据解方程,可得F点坐标,平移后的对称轴,根据平移后的对称轴,可得平移后的函数解析式;
(3)根据图象平移的规律,可得A′,C′,D′′点的坐标,根据待定系数法,可得A′C,BC,C′D′的解析式,根据解方程组,可得M、N的坐标,根据平行四边形的判定,可得四边形CMNC′的形状,根据平行四边形的面积公式,可得答案.
解答 解:(1)当y=0时,-$\frac{4}{21}$x2+$\frac{16}{21}$x+4=0,
解得x1=-3,x2=7,
∴点A坐标为(-3,0),点B的坐标为(7,0).
∵-$\frac{b}{2a}$=-$\frac{\frac{16}{21}}{2×(-\frac{4}{21})}$,
∴抛物线w的对称轴为直线x=2,
∴点D坐标为(2,0).
当x=0时,y=4,
∴点C的坐标为(0,4).
设直线l的表达式为y=kx+b,
$\left\{\begin{array}{l}{b=4}\\{2k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
∴直线l的解析式为y=-2x+4;
(2)∵抛物线w向右平移,只有一种情况符合要求,
即∠FAC=90°,如图 .
.
此时抛物线w′的对称轴与x轴的交点为G,
∵∠1+∠2=90°∠2+∠3=90°,
∴∠1=∠3,
∴tan∠1=tan∠3,
∴$\frac{FG}{AG}$=$\frac{AO}{CO}$.
设点F的坐标为(xF,-2xF+4),
∴$\frac{-(-2{x}_{F}+4)}{{x}_{F}-(-3)}$=$\frac{3}{4}$,
解得xF=5,-2xF+4=-6,
∴点F的坐标为(5,-6),
此时抛物线w′的函数表达式为y=-$\frac{4}{21}$x2+$\frac{40}{21}$x;
(3)由平移可得:点C′,点A′,点D′的坐标分别为C′(m,4),A′(-3+m,0),D′(2+m,0),CC′∥x轴,C′D′∥CD,
可用待定系数法求得
直线A′C′的表达式为y=$\frac{4}{3}$x+4-$\frac{4}{3}$m,
直线BC的表达式为y=-$\frac{4}{7}$x+4,
直线C′D′的表达式为y=-2x+2m+4,
分别解方程组$\left\{\begin{array}{l}{y=\frac{4}{3}x+4-\frac{4}{3}m}\\{y=-2x+4}\end{array}\right.$和$\left\{\begin{array}{l}{y=-2x+2m+4}\\{y=-\frac{4}{7}x+4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2}{5}m}\\{y=-\frac{4}{5}m+4}\end{array}\right.$和$\left\{\begin{array}{l}{x=\frac{7}{5}m}\\{y=-\frac{4}{5}m+4}\end{array}\right.$,
∴点M的坐标为($\frac{2}{5}$m,-$\frac{4}{5}$m+4),点N的坐标为($\frac{7}{5}$m,-$\frac{4}{5}$m+4),
∴yM=yN∴MN∥x轴,
∵CC′∥x轴,
∴CC′∥MN.
∵C′D′∥CD,
∴四边形CMNC′是平行四边形,
∴S=m[4-(-$\frac{4}{5}$m+4)]=$\frac{4}{5}$m2
点评 本题考察了二次函数综合题,(1)利用了自变量与函数值的对应关系,待定系数法求函数解析式;(2)利用了余角的性质,正切函数的性质,利用等角的正切函数值相等得出关于F点横坐标的方程是解题关键;(3)利用了图象的平移规律,待定系数法求函数解析式,解方程组得出M、N的坐标是解题关键,又利用了平行四边形的判定,平行四边形的面积公式.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
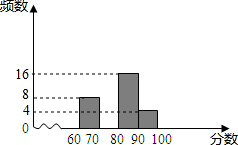 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图
为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图| 分数段(分手为x分) | 频数 | 百分比 |
| 60≤x<70 | 8 | 20% |
| 70≤x<80 | a | 30% |
| 80≤x≤90 | 16 | b% |
| 90≤x<100 | 4 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品牌 | 进价/(元/件) | 售价/(元/件) |
| A | 50 | 80 |
| B | 40 | 65 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
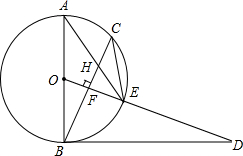 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com