
| 品牌 | 进价/(元/件) | 售价/(元/件) |
| A | 50 | 80 |
| B | 40 | 65 |
分析 (1)由总利润=A品牌T恤的利润+B品牌T恤的利润就可以求出w关于x的函数关系式;
(2)根据“两种T恤的总费用不超过9500元”建立不等式求出x的取值范围,由一次函数性质就可以求出结论.
解答 解:(1)设购进A种T恤x件,则购进B种T恤(200-x)件,由题意得:
w=(80-50)x+(65-40)(200-x),
w=30x+5000-25x,
w=5x+5000.
答:w关于x的函数关系式为w=5x+5000;
(2)∵购进两种T恤的总费用不超过9500元,
∴50x+40(200-x)≤9500,
∴0≤x≤150.
∵w=5x+5000.
∴k=5>0
∴w随x的增大而增大,
∴x=150时,w的最大值为5750.
∴购进A种T恤150件.
∴购进A种T恤150件,购进B种T恤50件可获得最大利润,最大利润为5750元.
点评 本题考查了由销售问题的数量关系求函数的解析式的运用,列一元一次不等式解实际问题的运用,一次函数的性质的运用,解答时求出函数的解析式是关键.


科目:初中数学 来源: 题型:选择题
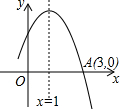 如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )
如图所示是二次函数y=ax2+bx+c图象的一部分,图象过A点(3,0),对称轴为x=1,给出四个结论:①b2-4ac>0;②2a+b=0;③a+b=0;④当x=-1或x=3时,函数y的值都等于0,其中正确结论是( )| A. | ②③④ | B. | ①③④ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于点E,垂足为D,CE平分∠ACB.若BE=2,则AE的长为( )| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
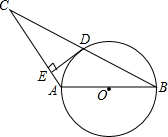 如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
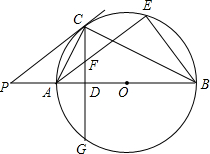 如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
如图,AB为⊙O的直径,P是BA延长线上一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com