
【题目】如图,△ABC中,AB=AC,tanB=![]() , BC=4,E为BA延长线上一点,⊙E过点C与射线BC的另一交点为F,射线EF与射线AC交于P
, BC=4,E为BA延长线上一点,⊙E过点C与射线BC的另一交点为F,射线EF与射线AC交于P
(1)求证:AE2=AP·AC
(2)当F点在线段BC上时,设CF=x,△PFC的面积为y,求y与x的函数关系式并写出x的取值范围
(3)当![]() 时求BE
时求BE

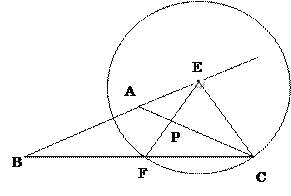
备用图
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】分析:![]() 证明△AEP∽△ACE,根据相似三角形的性质得到
证明△AEP∽△ACE,根据相似三角形的性质得到![]() ,即可证明.
,即可证明.
![]() 证明△ECB∽△PFC.得到
证明△ECB∽△PFC.得到![]() ,求出
,求出![]() ,即可得到y与x的函数关系式.
,即可得到y与x的函数关系式.
![]() 分①
分①![]() ②
②![]() 两种情况进行讨论.
两种情况进行讨论.
详解:(1)∵![]() ∴∠B=∠ACB
∴∠B=∠ACB
∵![]() ∴∠EFC=∠ECF
∴∠EFC=∠ECF
∵![]()
又∵![]()
∴∠BEF=∠ACE
∵![]()
∴△AEP∽△ACE.
∴![]() ∴
∴![]()
(2)∵∠B=∠ACB,∠ECF=∠EFC,
∴△ECB∽△PFC.
∴![]()
![]()
∵![]()
∴![]() .∴
.∴![]()
在Rt△BEH中,∵![]() ∴
∴![]() .
.
∴![]()
∴![]() .
.
∴![]()
(3) ①![]()
∵![]()
∴![]()
∵△AEP∽△ACE.
∴![]()
∴![]()
![]() .
.
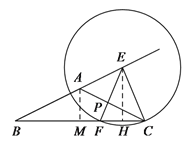
∵![]()
![]() ∴
∴![]()
在Rt△ABM中,∵![]() ∴
∴![]()
∴![]() ∴
∴![]()
②![]()
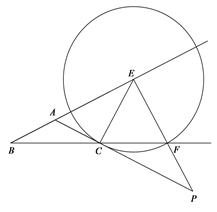
∵∠EFC=∠ECF,![]()
![]() .
.
又∵![]() ∴∠B =∠FCP.
∴∠B =∠FCP.
∴∠P =∠BEC.
∵![]()
∴△AEP∽△ACE,∴![]()
∵![]() ∴
∴![]()
∴![]()
∴![]() .
.
综上所述,![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点O与平面直角坐标系的原点重合,点A,C分别在x轴,y轴上,点B的坐标为(-5,4),点D为边BC上一点,连接OD,若线段OD绕点D顺时针旋转90°后,点O恰好落在AB边上的点E处,则点E的坐标为( )

A. (-5,3) B. (-5,4) C. (-5,![]() ) D. (-5,2)
) D. (-5,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,要测量一个沼泽水潭的宽度.现由于不能直接测量,小军是这样操作的:他在平地上选取一点C,该点可以直接到达A与B点,接着他量出AC和BC的距离,并找出AC与BC的中点E、F,连接EF,测量EF的长,于是他便知道了水潭AB的长等于2EF,小军的做法有道理吗?说明理由.你还有比小军更简单的方法吗?
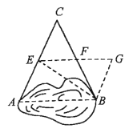
查看答案和解析>>
科目:初中数学 来源: 题型:
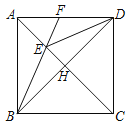
【题目】已知:如图,边长为1的正方形ABCD中,AC 、DB交于点H.DE平分∠ADB,交AC于点E.联结BE并延长,交边AD于点F.
(1)求证:DC=EC;
(2)求△EAF的面积.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导节约能源,自某日起,我国对居民用电采用阶梯电价,为了使大多数家庭不增加电费支出,事前就需要了解居民全年月平均用电量的分布情况,制订一个合理的方案.某调查人员随机调查了![]() 市
市![]() 户居民全年月平均用电量(单位:千瓦时)数据如下:
户居民全年月平均用电量(单位:千瓦时)数据如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表:
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合计 |
|
|
画出频数分布直方图,如下:

(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图,则不低于![]() 千瓦时的部分圆心角的度数为_____________;
千瓦时的部分圆心角的度数为_____________;
(3)若![]() 市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
市的阶梯电价方案如表所示,你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分別交于
轴分別交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一点.
上一点.
(1)求点![]() 、
、![]() 的坐标;
的坐标;
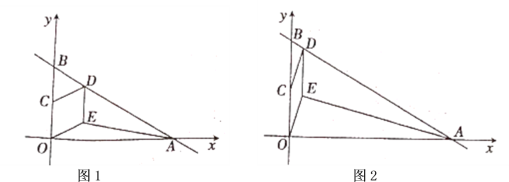
(2)若四边形![]() 是菱形,如图1,求
是菱形,如图1,求![]() 的面积;
的面积;
(3)若四边形![]() 是平行四边形,如图2,设点
是平行四边形,如图2,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学解方程的过程,请仔细阅读,并解答所提出的问题.
![]()
解:去分母,得![]() ,①
,①
去括号,得![]() ,②
,②
移项,得![]() ,③
,③
合并同类项,得![]() ,④
,④
系数化为![]() ,得
,得![]() .⑤
.⑤
(1)聪明的你知道小明的解答过程在________(填序号)处出现了错误,出现错误的原因是违背了__________.
A.等式的基本性质![]() ;B.等式的基本性质
;B.等式的基本性质![]() ;C.去括号法则;D加法交换律.
;C.去括号法则;D加法交换律.
(2)请你写出正确的解答过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=![]() .
.
(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:![]() +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com