
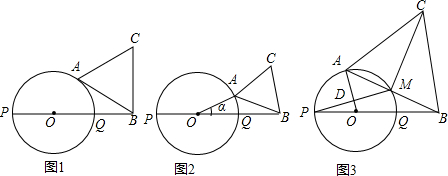
分析 (1)连接OA,如下图1,根据条件可求出AB.
(2)如下图2,首先考虑临界位置:当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;当线段AB所在的直线与圆O相切时,线段AB与圆O只有一个公共点,此时α=60°.从而定出α的范围.
(3)连接MQ,如下图3,易证AO∥MQ,从而得到△PNO∽△PMQ,△BMQ∽△BAO,又PO=OQ=BQ,从而可以求出MQ、ON,进而求出PN、NM、AM、CM的值.
解答 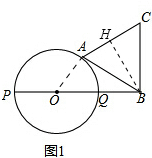 解:(1)如图1,连接OA,过点B作BH⊥AC,垂足为H,如图1所示.
解:(1)如图1,连接OA,过点B作BH⊥AC,垂足为H,如图1所示.
∵AB与⊙O相切于点A,
∴OA⊥AB.
∴∠OAB=90°.
∵OQ=QB=$\frac{1}{2}$,
∴OA=$\frac{1}{2}$,OB=OQ+QB=1.
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$;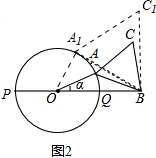 (2)①当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;
(2)①当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;
②当线段A1B所在的直线与圆O相切时,如图2所示,
线段A1B与圆O只有一个公共点,
此时OA1⊥BA1,OA1=$\frac{1}{2}$,OB=1,
∴cos∠A1OB=$\frac{{A}_{1}O}{OB}$=$\frac{1}{2}$.
∴∠A1OB=60°.
∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.
故答案为:0°≤α≤60°.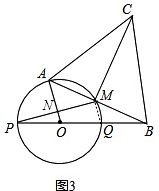 (3)连接MQ,如图3所示.
(3)连接MQ,如图3所示.
∵PQ是⊙O的直径,
∴∠PMQ=90°.
∵OA⊥PM,
∴∠PNO=90°.
∴∠PNO=∠PMQ.
∴ON∥MQ.
∴△PNO∽△PMQ.
∴$\frac{PN}{PM}=\frac{ON}{MQ}=\frac{PO}{PQ}$,
∵PO=OQ=$\frac{1}{2}$PQ.
∴PN=$\frac{1}{2}$PM,ON=$\frac{1}{2}$MQ.
同理:MQ=$\frac{1}{2}$AO,BM=$\frac{1}{2}$AB.
∵AO=$\frac{1}{2}$,
∴MQ=$\frac{1}{4}$.
∴ON=$\frac{1}{8}$.
∵∠PNO=90°,PO=$\frac{1}{2}$,ON=$\frac{1}{8}$,
∴PN=$\sqrt{O{P}^{2}-O{N}^{2}}$=$\frac{\sqrt{15}}{8}$.
∴PM=$\frac{\sqrt{15}}{4}$.
∴NM=PN=$\frac{\sqrt{15}}{8}$.
∵∠ANM=90°,AN=A0-ON=$\frac{3}{8}$,
∴AM=$\sqrt{A{N}^{2}+M{N}^{2}}$=$\frac{\sqrt{6}}{4}$.
∵△ABC是等边三角形,
∴AC=AB=BC,∠CAB=60°.
∵BM=$\frac{1}{2}$AB,
∴AM=BM.
∴CM⊥AB.
∵AM=$\frac{\sqrt{6}}{4}$,
∴BM=$\frac{\sqrt{6}}{4}$,AB=$\frac{\sqrt{6}}{2}$.
∴AC=$\frac{\sqrt{6}}{2}$.
∴CM=$\sqrt{A{C}^{2}-A{M}^{2}}$=$\frac{3\sqrt{2}}{4}$.
∴CM的长度为$\frac{3\sqrt{2}}{4}$.
点评 此题属于圆的综合题.考查了等边三角形的性质、相似三角形的性质与判定、切线的性质、勾股定理以及特殊三角函数值等知识.注意准确作出辅助线,利用临界值法求角的取值范围是解此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
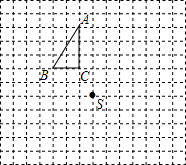 △ABC和点S都在正方形网格的格点上.
△ABC和点S都在正方形网格的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
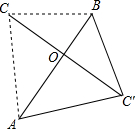 如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻折得到△ABC′的位置.
如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻折得到△ABC′的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数 | 100 | 95 | 90 | 85 | 80 | 75 |
| 人数 | 2 | 6 | 10 | 4 | 6 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com