
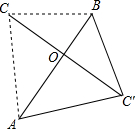
 如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻折得到△ABC′的位置.
如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻折得到△ABC′的位置.分析 (1)先证明AB垂直平分线段CC′,再利用$\frac{1}{2}$•AB•CO=$\frac{1}{2}$•AC•CB,求出OC即可.
(2)求出OB,根据S△BCC′=$\frac{1}{2}$•CC′•BO即可解决问题.
解答 解:(1) ∵BC=3,AC=4,AB=5,
∵BC=3,AC=4,AB=5,
∴BC2+AC2=AB2,
∴∠ACB=90°,
∵△ABC′是由△ABC翻折,
∴AB垂直平分CC′,
∴CO=C′O,
∵$\frac{1}{2}$•AB•CO=$\frac{1}{2}$•AC•CB,
∴CO=$\frac{AC•BC}{AB}$=$\frac{12}{5}$,
∴CC′=$\frac{24}{5}$.
(2)在RT△BOC中,∵∠COB=90°,BC=3,CO=$\frac{12}{5}$,
∴BO=$\sqrt{B{C}^{2}-C{O}^{2}}$=$\frac{9}{5}$,
∴S△BCC′=$\frac{1}{2}$•CC′•BO=$\frac{1}{2}$×$\frac{24}{5}$×$\frac{9}{5}$=$\frac{108}{25}$.
点评 本题考查翻折变换、勾股定理的逆定理、三角形的面积等知识,利用翻折变换的性质是解决问题的关键,学会利用面积法求直角三角形斜边上的高,属于中考常考题型.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6≤a≤-$\frac{11}{2}$ | B. | -6<a≤-$\frac{11}{2}$ | C. | -6<a<-$\frac{11}{2}$ | D. | -6≤a<-$\frac{11}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
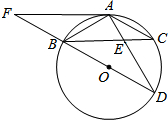 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com