
| 分数 | 100 | 95 | 90 | 85 | 80 | 75 |
| 人数 | 2 | 6 | 10 | 4 | 6 | 2 |
分析 (1)由加权平均数公式即可得出样本数据的平均数;由90分出现的次数最多得出众数;中位数等于第15个和第16个数据的平均数;
(2)求出获得100分的学员人数,即可得出小明被选中的概率.
解答 解:(1)本次随机抽取的样本数据的平均数=$\frac{100×2+95×6+90×10+85×4+80×6+75×2}{30}$=88(分);
众数为90(分);
中位数=$\frac{90+90}{2}$=90(分);
(2)∵获得100分的学员人数约为120×$\frac{2}{30}$=8,
∴小明被选中的概率为$\frac{1}{8}$.
点评 本题考查了众数、中位数、平均数以及概率的求法;熟记众数、中位数、平均数的概念以及概率公式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
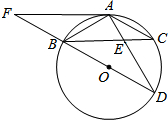 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,延长DB到F,使BF=BO,连接FA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com