
分析 若一元二次方程有两个相等的实数根,则根的判别式△=0,据此可求出b的值;进而可由三角形三边关系定理确定等腰三角形的三边长,即可求得其周长.
解答 解:∵关于x的方程x2+(b+2)x+6-b=0有两个相等的实数根,
∴△=(b+2)2-4(6-b)=0,即b2+8b-20=0;
解得b=2,b=-10(舍去);
①当a为底,b为腰时,则2+2<5,构不成三角形,此种情况不成立;
②当b为底,a为腰时,则5-2<5<5+2,能够构成三角形;
此时△ABC的周长为:5+5+2=12.
答:△ABC的周长是12.
点评 此题考查了根与系数的关系、等腰三角形的性质及三角形三边关系定理;在求三角形的周长时,不能盲目的将三边相加,而应在三角形三边关系定理为前提条件下分类讨论,以免造成多解、错解.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
| 分数 | 100 | 95 | 90 | 85 | 80 | 75 |
| 人数 | 2 | 6 | 10 | 4 | 6 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
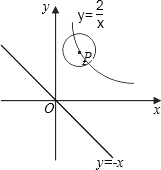 如图,直线y=-x与双曲线$y=\frac{2}{x}$(只在第一象限内的部分)在同一直角坐标系内,现有一个半径为1且圆心P在双曲线$y=\frac{2}{x}$上的一个动圆⊙P,⊙P在运动过程中圆上的点与直线y=-x的最近距离为1.
如图,直线y=-x与双曲线$y=\frac{2}{x}$(只在第一象限内的部分)在同一直角坐标系内,现有一个半径为1且圆心P在双曲线$y=\frac{2}{x}$上的一个动圆⊙P,⊙P在运动过程中圆上的点与直线y=-x的最近距离为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com