
����Ŀ��Ϊ�ḻѧ�����������ijУ�ƻ���������ѡ�γ̣����֡������赸���鷨���ݽ���Ҫ��ÿ��ѧ������ѡ����ֻ��ѡ��һ�ſγ̣�Ϊ��֤�ƻ�����Чʵʩ��ѧУ����Բ���ѧ��������һ�ε��飬�������������Ƴ���ͼ��������ͳ��ͼ�������ͳ��ͼ����������⣮
��1�����ν����ʾ������ѧ������ ������
��2����ȫ����ͳ��ͼ��
��3������ͳ��ͼ��ѡ�ޡ��ݽ����γ�����Ӧ���ε�Բ�ĽǵĶ���Ϊ�� ����
��4����У��800��ѧ�����������ѡ�ޡ����γ̵�ѧ���ж�������
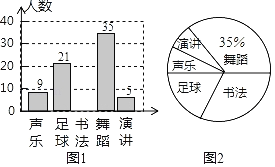
���𰸡���1��100����2������������3��18�㣻��4������ѡ�ޡ����γ̵�ѧ����168����
��������
��1�������赸����������ռ�İٷֱȼ���������ν����ʾ������ѧ������
��2������������ȥ�����γ̵����������ϲ���鷨���������Ӷ���ȫͳ��ͼ��
��3����360�����ѡ�ޡ��ݽ�����������ռ�İٷֱȼ��ɣ�
��4���ø�У������������ѡ�ޡ�����������ռ�İٷֱȼ��ɵó��𰸣�
�⣺��1�����ν����ʾ������ѧ���У�35��35%��100��������
�ʴ�Ϊ��100��
��2��ϲ���鷨�������У�100��9��21��35��5��30���ˣ���
��ȫͳ��ͼ���£�

��3������ͳ��ͼ��ѡ�ޡ��ݽ����γ�����Ӧ���ε�Բ�ĽǵĶ���Ϊ��360���![]() ��18�㣻
��18�㣻
�ʴ�Ϊ��18�㣻
��4����������ã�
800��![]() ��168��������
��168��������
�𣺹���ѡ�ޡ����γ̵�ѧ����168����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬������![]() ����A��-5��0����
����A��-5��0����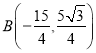 ���㣬����AB��BO��
���㣬����AB��BO��
��1���������߱���ʽ��
��2����C�ǵ��������ڵ�һ�����㣬����AOC���AOBȫ�ȣ���ֱ��д����C����______��
��3������D�ӵ�O�������߶�OA���A�������˶����ٶ�Ϊÿ��1����λ���ȣ�ͬʱ�߶�OA����һ����H�ӵ�A�������߶�AO���O�������˶����ٶ�Ϊÿ��2����λ���ȣ�����H�����Oʱ����DҲͬʱֹͣ�˶���������D��x��Ĵ��ߣ���ֱ��OB���ڵ�E���ӳ�DE����F��ʹ��EF=DE����DFΪ�ߣ���DF������ȱ�������DGF������D�˶�ʱ����G����FҲ��֮�˶���������H��x��Ĵ��ߣ���ֱ��AB���ڵ�L���ӳ�HL����M��ʹ��LM=HL����HMΪ�ߣ���HM���Ҳ����ȱ�������HMN������H�˶�ʱ����M����NҲ��֮�˶���������D�˶�t��ʱ����DGF��һ��������ֱ��ǡ�ù���HMN�����ģ�ֱ��д���˿�t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ������C�ڰ�Բ�ϣ���D��Բ�⣬DE��AB�ڵ�E��AC�ڵ�F����DF��CD
��1����֤��CD����O�����ߣ�
��2������F��AC���е㣬DF��2EF��2![]() ������O�뾶��
������O�뾶��
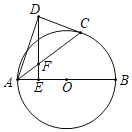
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
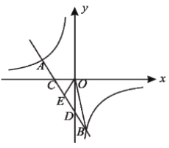
����Ŀ��˫����![]() ��kΪ��������
��kΪ��������![]() ����ֱ��
����ֱ��![]() ����
����![]() ����.
����.
��1����k��b��ֵ��
��2����ͼ��ֱ��AB��x���ڵ�C����y���ڵ�D������EΪCD���е㣬����BOE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
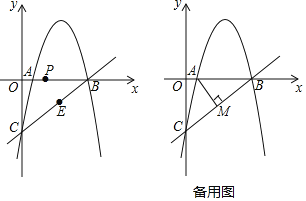
����Ŀ����ͼ��������![]() ����x���ϵĵ�A��1��0���͵�B��y���ϵĵ�C������B��C�����ֱ��Ϊ
����x���ϵĵ�A��1��0���͵�B��y���ϵĵ�C������B��C�����ֱ��Ϊ![]() ��
��
���������ߵĽ���ʽ��
�ڵ�P��A���������߶�AB����ÿ��1����λ���ٶ���B�˶���ͬʱ��E��B���������߶�BC����ÿ��2����λ���ٶ���C�˶���������һ���㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����PBE��������������ֵ��
�۹���A��![]() �ڵ�M������������һ����N�������B��C�غϣ���ֱ��AM��ƽ���߽�ֱ��BC�ڵ�Q������A��M��N��QΪ������ı�����ƽ���ı��Σ����N�ĺ����꣮
�ڵ�M������������һ����N�������B��C�غϣ���ֱ��AM��ƽ���߽�ֱ��BC�ڵ�Q������A��M��N��QΪ������ı�����ƽ���ı��Σ����N�ĺ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2+2x+c��y�ύ�ڵ�A����x�ύ�ڵ�B��3��0����C����1��0�����㣮
��1����ֱ��AB�������ߵı���ʽ��
��2������FΪֱ��AB�Ϸ���������һ���㣨����A��B�غϣ�������F��FP//x�ύֱ��AB�ڵ�P������F��FR//y�ύֱ��AB�ڵ�R����PR�����ֵ��
��3��������BA���ŵ�B��ʱ����ת90��õ�����BM����E������BM�˶��������B�غϣ�����BC��BEΪ�ڱ���ƽ���ı���BCDE����HΪDE���϶��㣬����CH����ֱ��д��CH+![]() HE����Сֵ��
HE����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
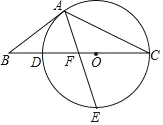
����Ŀ�� ��ͼ����O�ڡ�ABC��BC���ϣ���O������A��C������BC�ཻ�ڵ� D����E���°�Բ�����е㣬����AE��BC�ڵ�F����֪AB��BF��
��1����֤��AB�ǡ�O�����ߣ�
��2����OC��3��OF��1����cosB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ӱ�죬ij���߲˵ļ۸�������ǣ���ԭ�۵�1.5����ͬ����48Ԫ�����߲˱�ԭ������2ǧ�ˣ�
��1���������߲˵�ԭ����ÿǧ�˶���Ԫ��
��2��������ȡ���Ӳɹ����������������ȶ��ִ�ʩ�������ؼۣ������ϰ��յ���������߲˵����ļ������µ�����ÿǧ��10Ԫ��Ϊÿǧ��6.4Ԫ����ƽ��ÿ���µ��İٷ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �У�
�У�![]() Ϊ�Խ���
Ϊ�Խ���![]() ������һ�㣨����
������һ�㣨����![]() �غϣ�����
�غϣ�����![]() ������M��
������M��![]() ��
��![]() ����
����![]() ���ӳ��ߣ��ڵ�
���ӳ��ߣ��ڵ�![]() ������
������![]() ��
��
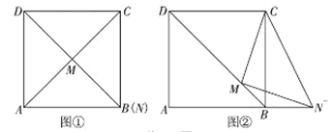
��֪����ͼ������MΪ![]() �е�ʱ������֤
�е�ʱ������֤![]() ������֤������
������֤������
̽������ͼ������MΪ�Խ���![]() ������һ�㣨����
������һ�㣨����![]() �غϣ���̽��
�غϣ���̽��![]() ��
��![]() ��������ϵ����֤����Ľ��ۣ�
��������ϵ����֤����Ľ��ۣ�
Ӧ�ã���1��ֱ��д��![]() �����S��ȡֵ��Χ��
�����S��ȡֵ��Χ��
��2����![]() ����
����![]() ��
��![]() ��������ϵ��_____________��
��������ϵ��_____________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com