
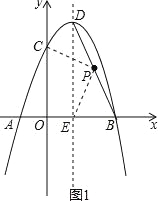
【题目】(2016广东省茂名市第25题)如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.
(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.

【答案】(1)、y=﹣x2+2x+3;(2)、(2,2);(3)、(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
试题分析:(1)、利用待定系数法求出过A,B,C三点的抛物线的函数表达式;(2)、连接PC、PE,利用公式求出顶点D的坐标,利用待定系数法求出直线BD的解析式,设出点P的坐标为(x,﹣2x+6),利用勾股定理表示出PC2和PE2,根据题意列出方程,解方程求出x的值,计算求出点P的坐标;(3)、设点M的坐标为(a,0),表示出点G的坐标,根据正方形的性质列出方程,解方程即可.
试题解析:(1)、∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,
∴![]() , 解得,
, 解得,![]() , ∴经过A,B,C三点的抛物线的函数表达式为y=﹣x2+2x+3;
, ∴经过A,B,C三点的抛物线的函数表达式为y=﹣x2+2x+3;
(2)、如图1,连接PC、PE, x=﹣![]() =﹣
=﹣![]() =1, 当x=1时,y=4,
=1, 当x=1时,y=4,
∴点D的坐标为(1,4), 设直线BD的解析式为:y=mx+n,则![]() , 解得,
, 解得,![]() ,
,
∴直线BD的解析式为y=﹣2x+6, 设点P的坐标为(x,﹣2x+6),
则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2, ∵PC=PE,
∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2, 解得,x=2, 则y=﹣2×2+6=2, ∴点P的坐标为(2,2);
(3)、设点M的坐标为(a,0),则点G的坐标为(a,﹣a2+2a+3),
∵以F、M、G为顶点的四边形是正方形, ∴FM=MG,即|2﹣a|=|﹣a2+2a+3|,
当2﹣a=﹣a2+2a+3时, 整理得,a2﹣3a﹣1=0, 解得,a=![]() ,
,
当2﹣a=﹣(﹣a2+2a+3)时, 整理得,a2﹣a﹣5=0, 解得,a=![]() ,
,
∴当以F、M、G为顶点的四边形是正方形时,点M的坐标为(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】下列四个命题:
①一组对边平行且一组对角相等的四边形是平行四边形;
②对角线互相垂直且相等的四边形是正方形;
③顺次连接矩形四边中点得到的四边形是菱形;
④正五边形是轴对称图形,其中真命题有( )
A.①②③B.①③④C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
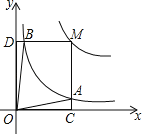
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
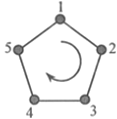
【题目】如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”. 如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,那么第二次“移位”后他所处的顶点的编号为____________。第181次“移位”后,则他所处顶点的编号是___________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(1)![]()
(2)![]()
(3)![]() (简便算法)
(简便算法)
(4)![]()
(5)![]()
(6)![]()
(7)(2b-3c+4)(3c-2b+4)
(8)[(x-y)2-(x + y)2]÷(-4xy)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com