
 直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P.
直线MN表示一条河流的河岸,在河流同旁有A、B两个村庄,现要在河边修建一个供水站给A、B供水.问:这个供水站建在什么地方,可以使铺设管道最短?请在图中找出表示供水站的点P. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
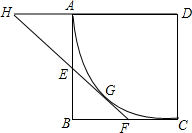 如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.
如图,正方形ABCD的边长为6,以D为圆心,DA为半径作⊙D,E在AB上,EF切⊙D于G,交BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
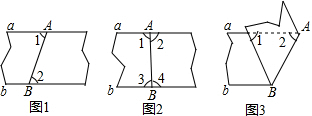
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
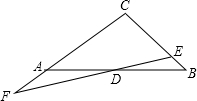 如图,△ABC中,D为边AB的中点,E为边BC上一点,ED延长线交CA延长线于点F,以下结论正确的有②④.
如图,△ABC中,D为边AB的中点,E为边BC上一点,ED延长线交CA延长线于点F,以下结论正确的有②④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com