
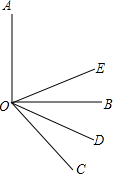
 如图,已知OE是∠AOC的平分线,OD是∠BOC的平分线,若∠AOB=90°,求∠DOE的度数.
如图,已知OE是∠AOC的平分线,OD是∠BOC的平分线,若∠AOB=90°,求∠DOE的度数. 分析 根据角平分线的定义以及角的和、差即可得到∠EOD=∠EOC-∠COD=$\frac{1}{2}$∠AOC-$\frac{1}{2}$BOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB,从而求解.
解答 解:∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠EOC=$\frac{1}{2}$∠AOC,∠COD=$\frac{1}{2}$∠BOC,
∴∠EOD=∠EOC-∠COD=$\frac{1}{2}$∠AOC-$\frac{1}{2}$BOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB=45°.
点评 本题考查了角度的计算,角平分线的定义,证明的∠EOD=$\frac{1}{2}$∠AOB是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果a<b,那么a-c<b-c | B. | 如果a>b,c>0,那么ac>bc | ||
| C. | 如果m<n,p<0,那么$\frac{m}{p}$>$\frac{n}{p}$ | D. | 如果x>y,z<0,那么xz>yz |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com