
 ���벢̽����
���벢̽�������� ��1������������εij��Ϳ��ֱ�Ϊx��y�������¾��ε��ܳ�������ֱ�����֪�����ܳ��������3�����г���������⼴�ɣ�
����������εij��Ϳ��ֱ�Ϊx��y�������¾��ε��ܳ�������ֱ�����֪�����ܳ��������$\frac{1}{3}$�����г���������⣬���á��ж��⣻
��2����������εij��Ϳ��ֱ�Ϊx��y����ʾ���й��ܳ������������������ϵʽ�����ú�����ͼ���ж��Ƿ���������ľ��μ��ɣ�
��3����������εij��Ϳ��ֱ�Ϊx��y��������������ϵʽ������õ������飬���÷��̡���0ʱ�����������ľ��μ��ɣ�
��� �⣺��1������������εij��Ϳ��ֱ�Ϊx��y��
����֪���εij��Ϳ��ֱ���2��1���¾��ε��ܳ�������ֱ�����֪�����ܳ��������3����
��$\left\{\begin{array}{l}{2��x+y��=3��2����2+1��}\\{xy=3��2��1}\end{array}\right.$�����$\left\{\begin{array}{l}{{x}_{1}=\frac{9+\sqrt{57}}{2}}\\{{y}_{1}=\frac{9-\sqrt{57}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=\frac{9-\sqrt{57}}{2}}\\{{y}_{2}=\frac{9+\sqrt{57}}{2}}\end{array}\right.$��
�������һ�����γ�Ϊ$\frac{9+\sqrt{57}}{2}$����Ϊ$\frac{9-\sqrt{57}}{2}$�������ܳ�������ֱ�����֪�����ܳ��������3����
����������εij��Ϳ��ֱ�Ϊa��b��
����֪���εij��Ϳ��ֱ���2��1���¾��ε��ܳ�������ֱ�����֪�����ܳ��������$\frac{1}{3}$����
��$\left\{\begin{array}{l}{2��a+b��=\frac{1}{3}��2����2+1��}\\{ab=\frac{1}{3}��2��1}\end{array}\right.$����Ϊa2-a+$\frac{2}{3}$=0����=1-$\frac{8}{3}$��0���ɵ÷����⣬
�������һ�����γ�ʹ�����ܳ�������ֱ�����֪�����ܳ��������$\frac{1}{3}$����
��2����������εij��Ϳ��ֱ�Ϊx��y��
����֪���εij��Ϳ��ֱ���2��1���¾��ε��ܳ�������ֱ�����֪�����ܳ��������3����
��2��x+y��=3��2����2+1����xy=3��2��1
��y=-x+9��y=$\frac{3}{x}$��
��ͼ��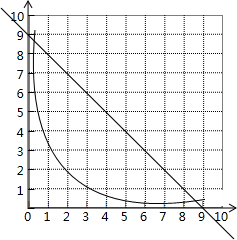
����ͼ��֪�������������Σ���ʹ���¾�����ԭ���ε��ܳ��������3����
��3����������εij��Ϳ��ֱ�Ϊx��y��
����֪���εij��Ϳ��ֱ���m��n���¾��ε��ܳ�������ֱ�����֪�����ܳ��������$\frac{1}{3}$����
��2��x+y��=$\frac{1}{3}$��2����m+n����xy=$\frac{1}{3}$��mn����ʽ�����ɵ�x2-$\frac{1}{3}$��m+n��x+$\frac{1}{3}$mn=0��
��=[$\frac{1}{3}$��m+n��]2-4��$\frac{1}{3}$mn��0������m2+n2-10mn��0��
�൱m2+n2-10mn��0ʱ��������һ������ʹ�����ܳ�������ֱ�����֪�����ܳ��������$\frac{1}{3}$����
���� ���⿼���˷�����������Ӧ�ã�����Ĺؼ��ǻ��������ú���ͼ������壬�Լ�ͼ����ص㣬�����йᴩ�˷���˼������ν�ϵ�˼�룬��ע����ᣮ


 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
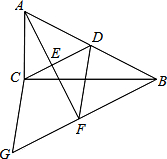 ��ͼ���ڡ�ABC�У���ACB=90�㣬CDΪAB���ϵ����ߣ�����A��AE��CD�ڵ�E������B��CDƽ���ߣ���AE���ӳ����ڵ�F�����ӳ����Ͻص�FG=CD������CG��DF����BG=11��AF=8�����ı���CGFD���������20��
��ͼ���ڡ�ABC�У���ACB=90�㣬CDΪAB���ϵ����ߣ�����A��AE��CD�ڵ�E������B��CDƽ���ߣ���AE���ӳ����ڵ�F�����ӳ����Ͻص�FG=CD������CG��DF����BG=11��AF=8�����ı���CGFD���������20���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
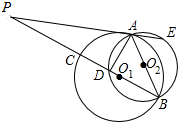 ��ͼ����֪��O1���O2�ཻ��A��B���㣬AB�ǡ�O2��ֱ������A������O1�����߽���O2�ڵ�E������BO1���ӳ��߽��ڵ�P��PB�ֱ����O1����O2����C��D���㣬��֤��
��ͼ����֪��O1���O2�ཻ��A��B���㣬AB�ǡ�O2��ֱ������A������O1�����߽���O2�ڵ�E������BO1���ӳ��߽��ڵ�P��PB�ֱ����O1����O2����C��D���㣬��֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
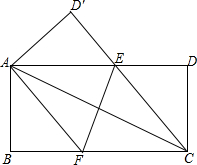 ��ͼ����һ�ž���ֽƬ�У�AB=4��BC=8����E��F�ֱ��ڱ�AD��BC�ϣ���ֽƬABCD��ֱ��EF�۵�����Cǡ�����A�غϣ���D���ڵ�D�䴦
��ͼ����һ�ž���ֽƬ�У�AB=4��BC=8����E��F�ֱ��ڱ�AD��BC�ϣ���ֽƬABCD��ֱ��EF�۵�����Cǡ�����A�غϣ���D���ڵ�D�䴦�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com