
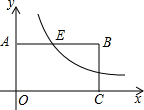
 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴上,以OA、OC为边作矩形OABC,双曲线y=$\frac{6}{x}$(x>0)交AB于点E,AE:EB=1:3.则矩形OABC的面积是24.
如图,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴上,以OA、OC为边作矩形OABC,双曲线y=$\frac{6}{x}$(x>0)交AB于点E,AE:EB=1:3.则矩形OABC的面积是24. 分析 根据反比例函数图象上点的坐标特征设E点坐标为(t,$\frac{6}{t}$),则利用AE:EB=1:3,B点坐标可表示为(4t,),然后根据矩形面积公式计算.
解答 解:设E点坐标为(t,$\frac{6}{t}$),
∵AE:EB=1:3,
∴B点坐标为(4t,$\frac{6}{t}$),
∴矩形OABC的面积=4t•$\frac{6}{t}$=24.
故答案为:24.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=$\frac{k}{x}$(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.


科目:初中数学 来源: 题型:选择题
| A. | 方差越大,说明数据就越稳定 | |
| B. | 有一个锐角相等的两个直角三角形相似 | |
| C. | 在不等式两边同乘以或同除以一个不为0的数时,不等号的方向不变 | |
| D. | 两边及其一边的对角对应相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
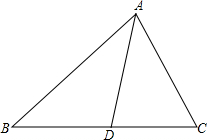 如图,小明和小刚住在同一小区(A点),每天一块去学校(B点)上学,一天,小明要先去文具店(C点)买练习本再去学校,小刚要先去书店(D点)买书再去学校,问:这天两人从家到学校谁走的路远?为什么?
如图,小明和小刚住在同一小区(A点),每天一块去学校(B点)上学,一天,小明要先去文具店(C点)买练习本再去学校,小刚要先去书店(D点)买书再去学校,问:这天两人从家到学校谁走的路远?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
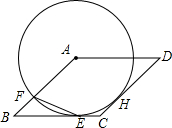 如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF
如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y1>y2 | D. | y2>y1>y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com