
���� ����̽����������֪�����жϼ��ɣ�
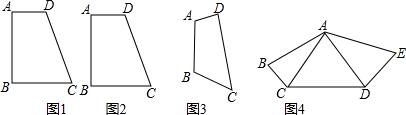
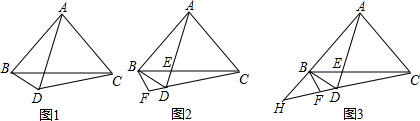
������죺�������루1�����ƣ�����SAS֤����DAE�ա�EBC���ɣ�
��չ��Ӧ�ã���CD�Ͻ�ȡCF=DE��֤����BCF�ա�FDE����ABF�ա�AEF����ABC�ա�AFD���ɣ�
��� �⣺����̽������ͼ2����AB�Ͻ�ȡAE=BC������DE��CE��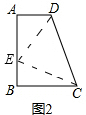
��AB=AD+BC��AE=BC��AB=AE+BE��
��AD=BE��
�ڡ�DAE�͡�EBC�У�
$\left\{\begin{array}{l}{AD=EB}\\{��A=��B}\\{AE=BC}\end{array}\right.$
���DAE�ա�EBC��SAS����
��DE=CE����ADE=��CEB��
�ߡ�ADE+��AED=90�㣬
���CEB+��AEB=90��
��DE��CE��
�ʴ�Ϊ��SAS��=��
������죺��ͼ3����AB�Ͻ�ȡAE=BC������DE��CE��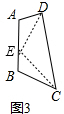
��AB=AD+BC��AE=BC��AB=AE+BE��
��AD=BE��
�ڡ�DAE�͡�EBC�У�
$\left\{\begin{array}{l}{AD=EB}\\{��A=��B}\\{AE=BC}\end{array}\right.$
���DAE�ա�EBC��SAS����
��DE=CE����AED=��ECB��
�ߡ�AEC=��DEC+��AED����AEC=��B+��ECB��
���B=��DEC��
��չ��Ӧ�ã�
��ACD�ǵȱ������Σ�
���ɣ���ͼ4����CD�Ͻ�ȡCF=DE������AF��BF��EF��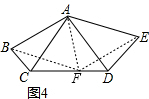
��BC+DE=CD��CF+DF=CD��
��BC=DF��
�ڡ�BCF�͡�FDE�У�
$\left\{\begin{array}{l}{BC=FD}\\{��BCF=��FDE}\\{CF=DE}\end{array}\right.$
���BCF�ա�FDE��
��BF=FE����CBF=��DFE��
�ߡ�CBF+��BFC=180��-��BCD=180��-120��=60�㣬
���EFD+��BCF=60�㣬
���BFE=180��-����EFD+��BCF��=120�㣬
�ڡ�ABF�͡�AEF�У�
$\left\{\begin{array}{l}{AB=AE}\\{BF=FE}\\{AF=AF}\end{array}\right.$
���ABF�ա�AEF��
���BAF=��EAF����BFA=��EFA��
�ߡ�BAE=120�㣬��BFE=120��
���BAF=��EAF=60�㣬��BFA=��EFA=60�㣬
���ABF�ǵȱ������Σ�
��AB=AF����ABF=60�㣬
���ABF+��CBF=��AFE+��CFE��
����ABC=��AFD��
�ڡ�ABC�͡�AFD�У�
$\left\{\begin{array}{l}{AB=AF}\\{��ABC=��AFD}\\{BC=DF}\end{array}\right.$
���ABC�ա�AFD��
��AC=AD����BAC=��FAD��
���BAC+��CAF=��FAD+��CAF=��BAF=60�㣬
���ACD�ǵȱ������Σ�
���� ���⿼����ȫ�������ε����ʶ������ж��������ȱ������ε��ж��������������Ĺؼ������������ߣ�����ȫ�������Σ�


 ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д� ���⿼����Ԫ���Ծ�ϵ�д�
���⿼����Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
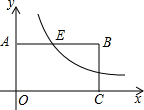 ��ͼ����ƽ��ֱ������ϵ�У���A�͵�C�ֱ���y���x���������ϣ���OA��OCΪ��������OABC��˫����y=$\frac{6}{x}$��x��0����AB�ڵ�E��AE��EB=1��3�������OABC�������24��
��ͼ����ƽ��ֱ������ϵ�У���A�͵�C�ֱ���y���x���������ϣ���OA��OCΪ��������OABC��˫����y=$\frac{6}{x}$��x��0����AB�ڵ�E��AE��EB=1��3�������OABC�������24���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
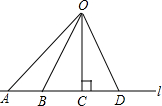 ��ͼ�������߶��У���̵��ǣ�������
��ͼ�������߶��У���̵��ǣ�������| A�� | �߶�OA | B�� | �߶�OB | C�� | �߶�OC | D�� | �߶�OD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a-2c | B�� | 2b | C�� | 2a | D�� | 2b-2a |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com