
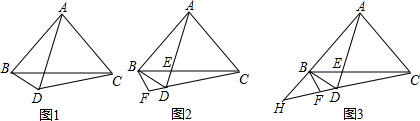
分析 (1)如图1中,作CE⊥BD的延长线于E,AH⊥BC于H,EF⊥BC于F,取AC中点G,连接DC、DG、FG,先证明E、F、G三点共线,再证明D、G、C、E四点共圆,即可证明△ACD是等边三角形解决问题.
(2)如图2中,结论:DF=DE.在BC上截取BN=BF,先证明△DBN≌△DBF,得DF=DN,再证明DN=DE即可.
(3)如图3中,连接EF,作EQ⊥AB于Q,先证明AE=HF,HB=HF,然后在RT△AQE中理由30度角的性质即可就问题.
解答 (1)证明:如图1中,作CE⊥BD的延长线于E,AH⊥BC于H,EF⊥BC于F,取AC中点G,连接DC、DG、FG.
∵AB=AC,
∴BH=CH=$\frac{1}{2}$BC,
∵∠CEF+∠BCE=∠CBE+∠BCE=90°,
∴∠CEF=∠CBE=30°,
∵CE=$\frac{1}{2}$BC=CH,
又∵CF=$\frac{1}{2}$CE=$\frac{1}{2}CH$,
∴点F是CH中点,
∵第G是AC中点,
∴FG∥AH,
∵AH⊥BC,∴FG⊥BC于F,又EF⊥BC于F,
∴E、F、G三点共线,
∵的D在线段AC的垂直平分线上,
∴DG⊥AC,AD=CD,∠ADG=∠CDG,
∴∠DGC=∠CED=90°,
∴D、G、C、E四点共圆,
∴∠CDG=∠CED=30°,
∴∠ADC=2∠CDG=60°,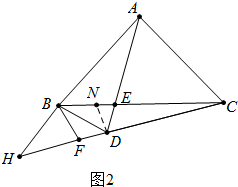
∴△ADC是等边三角形,
∴AD=AC=DC,∵AB=AC,
∴AB=AD.
(2)如图2中,结论:DF=DE.
理由:在BC上截取BN=BF,
在△BDN和△BDF中,
$\left\{\begin{array}{l}{BD=BD}\\{∠DBN=∠DBF}\\{BN=BF}\end{array}\right.$,
∴△DBN≌△DBF,
∴DN=DF,∠BFD=∠BND,
∵∠ADC=∠EBF,
∴B、F、D、E四点共圆,
∴∠BFD+∠BED=180°,
∵∠BND+∠DNE=180°,
∴∠DNE=∠DEN,
∴DN=DE,
∴DF=DE.
(3)如图3中,连接EF,作EQ⊥AB于Q.
∵DE=DF,∠ADC=60°,
∴∠DFE=∠DEF=30°,
∵∠H=30°,
∴∠H=∠DFE,
∴EF∥AB,
∴∠DAH=∠DEF=30°=∠H,
∴∠BAC=∠DAH+∠DAC=90°,
∵AB=AC,
∴∠ABC=∠ACB=45°,
∴DH=DA,
∵DE=DF,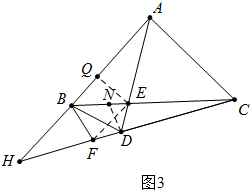
∴FH=AE,
∵∠H=30°,∠FBH=180°-∠ABC-∠CBF=75°,
∴∠BFH=180°-∠H-∠HBF=75°,
∴∠HBF=∠HFB,
∴HB=HF=AE=b,
在RT△AQE中,∵AE=b,∠QAE=30°,
∴QE=$\frac{1}{2}$b,
∵S△ABE=a
∴$\frac{1}{2}$•AB•QE=a,
∴AB=$\frac{4a}{b}$.
点评 本题考查四点共圆的判定和性质、全等三角形的判定和性质、直角三角形中30度角的性质、第一个问题的证明关键是添加辅助线构造四点共圆,第二个问题也是利用四点共圆的性质证明角相等,综合性比较强,属于中考压轴题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
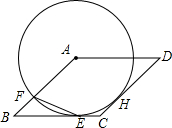 如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF
如图,⊙A与菱形ABCD的边BC相切于点E,与边AB相交于点F,连结EF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
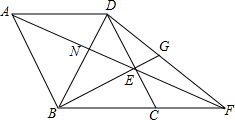 如图,在菱形ABCD中,∠ABC=120°,点E在边CD上(DE>CE),连结AE并延长交BC的延长线于点F,连结DF,连结BE并延长交DF于点G.若BE:EG=49:15,CF=6,则线段DN的长为$\frac{50}{13}$.
如图,在菱形ABCD中,∠ABC=120°,点E在边CD上(DE>CE),连结AE并延长交BC的延长线于点F,连结DF,连结BE并延长交DF于点G.若BE:EG=49:15,CF=6,则线段DN的长为$\frac{50}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25% | B. | 30% | C. | 15% | D. | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
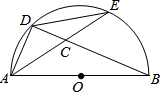 如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )
如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )| A. | ∠ACD=∠DAB | B. | AD=DE | C. | AD•AB=CD•BD | D. | AD2=BD•CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com