
【题目】提出问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
探究发现:如图所示,小敏用4个完全相同的、邻边长度分别为a、b的长方形拼成一个边长为(a+b)的正方形(其中a、b的和不变,但a、b的数值及两者的大小关系都可以变化).仔细观察拼图,我们发现,如果右图中间有空白图形F,那么它一定是正方形
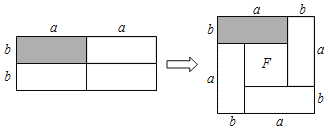
(1)空白图形F的边长为 ;
(2)通过计算左右两个图形的面积,我们发现(a+b)2、(a﹣b)2和ab之间存在一个等量关系式.
①这个关系式是 ;
②已知数x、y满足:x+y=6,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
问题解决:
问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
①对于周长一定的长方形,设周长是20,则长a和宽b的和是 面积S=ab的最大值为 ,此时a、b的关系是 ;
②对于周长为L的长方形,面积的最大值为 .
活动经验:
周长一定的长方形,当邻边长度a、b满足 时面积最大.
【答案】探究发现:(1)a﹣b;(2)①(a+b)2﹣(a﹣b)2=4ab;②5或﹣5;问题解决:①10,25,a=b;②![]() L2;活动经验:a=b.
L2;活动经验:a=b.
【解析】
探究发现
(1)由图可知:空白图形F的边长为:a-b;
(2)①由矩形的性质得出左图形的面积为:2a×2b=4ab,由正方形的性质得出右图形的面积为:(a+b)2-(a-b)2,即可得出答案;
②由①得出(x-y)2=25,即可得出答案;
问题解决
①由长方形的性质得出a+b=10,面积S=ab=a(10-a)=-a2+10a=-(a-5)2+25,由二次函数的性质即可得出答案;
②由长方形的性质得出面积![]() ;由二次函数的性质即可得出答案;
;由二次函数的性质即可得出答案;
活动经验
根据前面的问题即可得出结论.
(1)由图可知:空白图形F的边长为:a﹣b,
故答案为:a﹣b;
(2)①左图形的面积为:2a×2b=4ab,
右图形的面积为:(a+b)2﹣(a﹣b)2,
∴(a+b)2﹣(a﹣b)2=4ab,
故答案为:(a+b)2﹣(a﹣b)2=4ab;
②由(a+b)2﹣(a﹣b)2=4ab得:(x+y)2﹣(x﹣y)2=4xy,
即:62﹣(x﹣y)2=4×![]() ,
,
∴(x﹣y)2=25,
∴x﹣y=5或x﹣y=﹣5,
故答案为:5或﹣5;
问题解决:
解:①∵长方形的周长是20,
∴2(a+b)=20,
∴a+b=10,则b=10﹣a,
∴面积S=ab=a(10﹣a)=﹣a2+10a=﹣(a﹣5)2+25,
∴a=5时,S=ab的最大值为25,
此时a、b的关系是a=b,
故答案为:10,25,a=b;
②对于周长为L的长方形,
设一边长为a,则邻边长为![]() ﹣a,
﹣a,
∴面积![]() ;
;
∴面积的最大值为![]() L2;
L2;
故答案为:![]() L2;
L2;
活动经验:
解:周长一定的长方形,当邻边长度a、b满足a=b时面积最大;
故答案为:a=b.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为提供节约用水,某市按如下规定每月收取水费,若一户居民每月用水不超过20立方米,则每立方米按3元收费;若超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费,若某户居民某月用水![]() 立方米.
立方米.
(1)试用含![]() (
(![]() >20)的代数式表示这户居民该月应缴的水费.
>20)的代数式表示这户居民该月应缴的水费.
(2)已知该市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家这三个月应缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
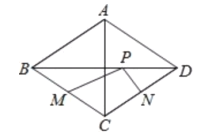
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
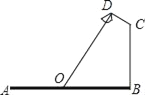
【题目】如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
A. (11﹣2![]() )米 B. (11
)米 B. (11![]() ﹣2
﹣2![]() )米 C. (11﹣2
)米 C. (11﹣2![]() )米 D. (11
)米 D. (11![]() ﹣4)米
﹣4)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运算律是解决许多数学问题的基础,在运算中有重要的作用,充分运用运算律能使计算简便高效.
例如:(-125![]() )÷(-5)
)÷(-5)
解:(-125![]() )÷(-5)=125
)÷(-5)=125![]() ×
×![]() =(125+
=(125+![]() )×
)×![]() =125×
=125×![]() +
+![]() ×
×![]() =25+
=25+![]() =25
=25![]()
(1)计算:6÷(-![]() +
+![]() ),A同学的计算过程如下:
),A同学的计算过程如下:
原式=6×(-![]() )+6×
)+6×![]() =-6+9=3.
=-6+9=3.
请你判断A同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考例题,用运算律简便计算(请写出具体的解题过程):
999×118![]() +333×(-
+333×(-![]() )-999×18
)-999×18![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个不同的数用大括号围起来,中间用逗号断开,如:{3,4},{-3,6,8,18},我们称之为集合,其中大括号内的数称其为集合的元素,如果一个集合满足:只要其中有一个元素a,使得-2a+4也是这个集合的元素,这样的集合我们称为条件集合,例如:集合{3,2},因为-2×3+4=-2,-2恰好是这个集合的元素,所以{3,-2}是条件集合:例如:集合{-2,9,8},因为-2×(-2)+4=8,8恰好是这个集合的元素,所以{-2,9,8}是条件集合.
(1)集合{-4,12}______条件集合;集合{![]() ,-
,-![]() ,
,![]() }______条件集合 (填“是”或“不是”)
}______条件集合 (填“是”或“不是”)
(2)若集合{8,10,n}是条件集合,求n的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了美化环境,计划分两次购进A,B两种花,第一次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花的数量不多于A种花的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com