
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
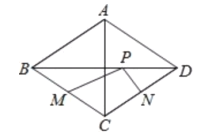
A.![]() B.3
B.3
C.![]() D.5
D.5
【答案】D
【解析】
作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,根据菱形的性质求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.
解:作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,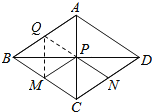
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,
即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,P是BD中点,
∵四边形ABCD是菱形,
∴CP=![]() AC=3,BP=
AC=3,BP=![]() BD=4,
BD=4,
在Rt△BPC中,由勾股定理得:BC=5,
即NQ=5,
∴MP+NP=QP+NP=QN=5,
故选:D.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2019个图中共有正方形的个数为( )
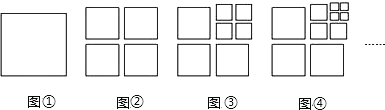
A.2019B.2021C.6049D.6055
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,直线l与直线AB、CD相交于点E、F,P是射线EA上的一个动点(不包括端点E),将△EFP沿PF折叠,便顶点E落在点Q处.若∠PEF=54°,且∠CFQ=![]() ∠CFP,则∠PFE的度数是_____.
∠CFP,则∠PFE的度数是_____.
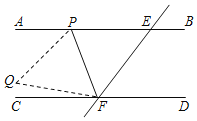
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为_____.正方形EDFC的面积为_______
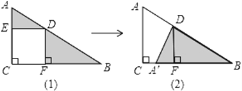
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
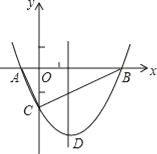
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,已知AD//BC,∠ABC=90°.

(1)若AC⊥BD,且AC=5,BD=3(如图1),求四边形ABCD的面积;
(2)若DE⊥BC于E,F是CD的中点,BD=BC,(如图2),求证:∠BAF=∠BCD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
探究发现:如图所示,小敏用4个完全相同的、邻边长度分别为a、b的长方形拼成一个边长为(a+b)的正方形(其中a、b的和不变,但a、b的数值及两者的大小关系都可以变化).仔细观察拼图,我们发现,如果右图中间有空白图形F,那么它一定是正方形
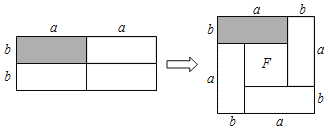
(1)空白图形F的边长为 ;
(2)通过计算左右两个图形的面积,我们发现(a+b)2、(a﹣b)2和ab之间存在一个等量关系式.
①这个关系式是 ;
②已知数x、y满足:x+y=6,xy=![]() ,则x﹣y= ;
,则x﹣y= ;
问题解决:
问题:“周长一定的长方形,当邻边长度满足什么条件时面积最大?”
①对于周长一定的长方形,设周长是20,则长a和宽b的和是 面积S=ab的最大值为 ,此时a、b的关系是 ;
②对于周长为L的长方形,面积的最大值为 .
活动经验:
周长一定的长方形,当邻边长度a、b满足 时面积最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第9个图形中,十字星与五角星的个数和为( )

A.28B.29C.31D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,平行四边形ABCD中,连接AC,AC=AB.过点B作BE⊥AC,垂足为E.延长BE与CD相交于点F:
(1)如图1,若AE=2.CE=1,求线段AD的长.
(2)如图2,若∠BAC=45°,过点F作FG⊥AD于点G,连接AF、EG,求证:BE+EC=![]() EG.
EG.
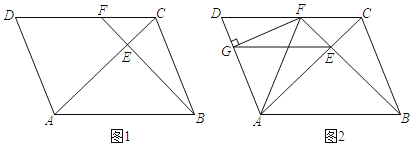
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com