
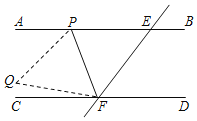
【题目】如图,直线AB∥CD,直线l与直线AB、CD相交于点E、F,P是射线EA上的一个动点(不包括端点E),将△EFP沿PF折叠,便顶点E落在点Q处.若∠PEF=54°,且∠CFQ=![]() ∠CFP,则∠PFE的度数是_____.
∠CFP,则∠PFE的度数是_____.
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示.
(1)求乙车离开A城的距离y关于t的函数解析式;
(2)求乙车的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
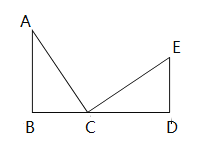
【题目】如图,在△ABC中,∠B=90°,点B、C、D在同一直线上,△ABC≌△CDE,且∠B=∠D,∠BAC=∠DCE.
(1)试说明BD=AB+ED;
(2)若∠CED=2∠BAC,求∠CED的度数;
(3)连接AE,则△ACE是怎样的三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)用“*”表示一种新运算:对于任意正实数a,b,都有![]() .例如,
.例如,![]() ,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
,那么15*27=__;(2)定义一种运算*,其规则为:当a≥b时,a*b=b3;当a<b时,a*b=b2.根据这个规则,方程3*x=27的解是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论错误的是( )

A.BP=CM
B.△ABQ≌△CAP
C.∠CMQ的度数不变,始终等于60°
D.当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形
秒时,△PBQ为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提供节约用水,某市按如下规定每月收取水费,若一户居民每月用水不超过20立方米,则每立方米按3元收费;若超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费,若某户居民某月用水![]() 立方米.
立方米.
(1)试用含![]() (
(![]() >20)的代数式表示这户居民该月应缴的水费.
>20)的代数式表示这户居民该月应缴的水费.
(2)已知该市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家这三个月应缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
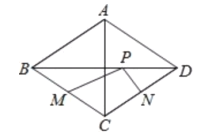
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com