
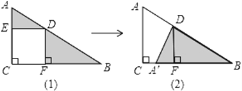
【题目】如图△ABC中有正方形EDFC,由图(1)通过三角形的旋转变换可以得到图(2).观察图形的变换方式,若AD=3,DB=4,则图(1)中△ADE和△BDF面积之和S为_____.正方形EDFC的面积为_______
【答案】6; ![]()
【解析】
由图形可知△DA′F是由△DAE旋转得到,利用旋转的性质可得到△A′DB为直角三角形,可求得S,在Rt△A′DB中 由勾股定理可求得A′B,再利用面积相等可求得DF,可求得正方形EDFC的面积.
解:由旋转的性质得AD=A′D=3,∠ADE=∠A′DF,
∵∠A′DB=∠A′DF+∠FDB=∠ADE+∠FDB=90°,
∴在Rt△A′DB中,
S△A′DB=![]() A′D×BD=
A′D×BD=![]() ×3×4=6,
×3×4=6,
∴S△ADE+S△BDF=S△A′DF+S△BDF=S△A′DB=6,
又A′D=3,BD=4,可求得A′B=5,
∴![]() A′BDF=
A′BDF=![]() ×5×DF=6,
×5×DF=6,
∴DF=![]() ,
,
∴S正方形EDFC=DF2=![]() ,
,
故答案为:6;![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校九年级甲、乙两班举行电脑汉字输入比赛,两个班能参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表:

有一位同学根据上面表格得出如下结论:
①甲、乙两班学生的平均水平相同;②乙班优秀人数比甲班优秀人数多(每分钟输入汉字达150个以上为优秀);③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.
上述结论正确的是_______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
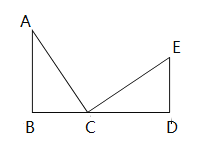
【题目】如图,在△ABC中,∠B=90°,点B、C、D在同一直线上,△ABC≌△CDE,且∠B=∠D,∠BAC=∠DCE.
(1)试说明BD=AB+ED;
(2)若∠CED=2∠BAC,求∠CED的度数;
(3)连接AE,则△ACE是怎样的三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论错误的是( )

A.BP=CM
B.△ABQ≌△CAP
C.∠CMQ的度数不变,始终等于60°
D.当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形
秒时,△PBQ为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提供节约用水,某市按如下规定每月收取水费,若一户居民每月用水不超过20立方米,则每立方米按3元收费;若超过20立方米,前20立方米收费标准不变,超过部分每立方米按5元收费,若某户居民某月用水![]() 立方米.
立方米.
(1)试用含![]() (
(![]() >20)的代数式表示这户居民该月应缴的水费.
>20)的代数式表示这户居民该月应缴的水费.
(2)已知该市小李家1月份用水13立方米,2月份用水22立方米,3月份用水17立方米,求他家这三个月应缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
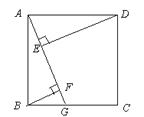
【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF;
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
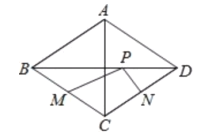
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运算律是解决许多数学问题的基础,在运算中有重要的作用,充分运用运算律能使计算简便高效.
例如:(-125![]() )÷(-5)
)÷(-5)
解:(-125![]() )÷(-5)=125
)÷(-5)=125![]() ×
×![]() =(125+
=(125+![]() )×
)×![]() =125×
=125×![]() +
+![]() ×
×![]() =25+
=25+![]() =25
=25![]()
(1)计算:6÷(-![]() +
+![]() ),A同学的计算过程如下:
),A同学的计算过程如下:
原式=6×(-![]() )+6×
)+6×![]() =-6+9=3.
=-6+9=3.
请你判断A同学的计算过程是否正确,若不正确,请你写出正确的计算过程.
(2)请你参考例题,用运算律简便计算(请写出具体的解题过程):
999×118![]() +333×(-
+333×(-![]() )-999×18
)-999×18![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正确的个数为( )
;其中正确的个数为( )
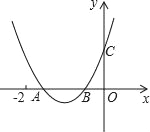
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com