
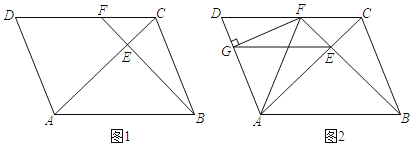
【题目】已知,平行四边形ABCD中,连接AC,AC=AB.过点B作BE⊥AC,垂足为E.延长BE与CD相交于点F:
(1)如图1,若AE=2.CE=1,求线段AD的长.
(2)如图2,若∠BAC=45°,过点F作FG⊥AD于点G,连接AF、EG,求证:BE+EC=![]() EG.
EG.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据垂直的定义得到∠AEB=∠BEC=90°,根据勾股定理得到BE=![]() ,BC=
,BC=![]() ,根据平行四边形的性质即可得到结果;
,根据平行四边形的性质即可得到结果;
(2)推出△AEB是等腰直角三角形,得到∠ABE=45°,设∠CBE=x,根据等腰三角形的性质得到∠ABC=∠ACB=45°+x,求得∠EBC=22.5°,∠ACB=67.5°,推出A、B、C、F四点共圆,A、E、F、G四点共圆,得到∠CAF=∠CBE=22.5°,∠EGF=∠EAF=22.5°,求得∠AGE=67.5°,推出AE=GE,根据等腰直角三角形的性质即可得到结论.
(1)解:∵BE⊥AC,
∴∠AEB=∠BEC=90°,
∵AE=2,CE=1,
∴AC=AB=3,
![]() ,
,
![]() ,
,
∵四边形ABCD是平行四边形,
∴AD=BC=![]() ;
;
(2)证明:∵BE⊥AC,
∴∠AEB=∠BEC=90°,
∵∠BAC=45°,
∴△AEB是等腰直角三角形,
∴∠ABE=45°,AE=BE,
∵AB∥CD,
∴∠ACF=45°,∠ABC+∠DCB=180°,
设∠CBE=x,
∴∠ABC=45°+x,
∵AB=AC,
∴∠ABC=∠ACB=45°+x,
∵∠EBC+∠ECB=90°,
∴x+45°+x=90°,
∴x=22.5°,
∴∠EBC=22.5°,∠ACB=67.5°,
∵∠ABF=∠ACF=45°,
∴A、B、C、F四点共圆,
∴∠CAF=∠EBC=22.5°,
∵FG⊥AD,
∴∠AGF=∠AEF=90°,
∴A、E、F、G四点共圆,
∴∠EGF=∠EAF=22.5°,
∴∠AGE=67.5°,
∵∠CAD=∠ACB=67.5°,
∴∠EAG=∠AGE,
∴AE=GE,
∵AC=AB=![]() AE,
AE,
∴BE+EC=AE+EC=AC=![]() EG.
EG.


科目:初中数学 来源: 题型:
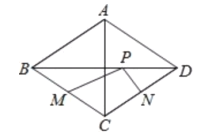
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣2(k﹣1)x+k2=0有两个实数根x1,x2.
(1)求k的取值范围;
(2)若|x1+x2|=x1x2﹣1,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
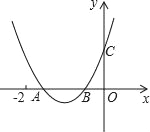
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正确的个数为( )
;其中正确的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆格力厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸r的范围为176≤r≤185的产品为合格),随机各抽取了20个样品进行检测,过程如下:
收集数据(单位:mm)
甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180
乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183
整理数据
级别 频数 | 165.5~ 170.5 | 170.5~ 175.5 | 175.5~ 180.5 | 180.5~ 185.5 | 185.5 ~190.5 | 190.5~ 195.5 |
甲车间 | 2 | 4 | a | b | 2 | 1 |
乙车间 | 1 | 2 | 9 | 6 | 2 | 0 |
分析数据:
车间 | 平均数 | 众数 | 中位数 | 方差 |
甲车间 | 180 | 185 | 180 | 43.1 |
乙车间 | 180 | 180 | c | 22.6 |
应用数据
(2)请写出表中a= ,b= ,c= mm.
(2)估计甲车间生产的1000个该款新产品中合格产品有多少个?
(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了美化环境,计划分两次购进A,B两种花,第一次分别购进A,B两种花30棵和15棵,共花费675元;第二次以同样的单价分别购进A、B两种花12棵和5棵,第二次花费265元.
(1)求A、B两种花的单价分别是多少元?
(2)若购买A、B两种花共31棵,且B种花的数量不多于A种花的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
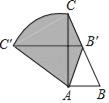
【题目】如图,在Rt△ABC中,∠B=60°,AB=1,现将△ABC绕点A逆时针旋转至点B恰好落在BC上的B'处,其中点C运动路径为![]() ,则图中阴影部分的面积是_____.
,则图中阴影部分的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元初,中美洲马雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“![]() ”、划“—”、卵形“
”、划“—”、卵形“![]() ”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1-19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
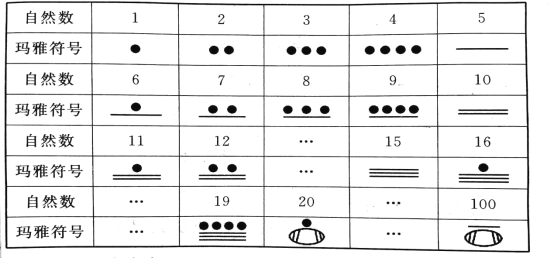
(1)玛雅符号![]() 表示的自然数是哪个数;
表示的自然数是哪个数;
(2)请你画出表示自然数280的玛雅符号.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com