Question

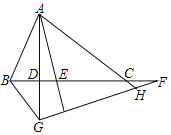
【题目】如图，△ABC中，AD⊥BC交BC于D，AE平分∠BAC交BC于E，F为BC的延长线上一点，FG⊥AE交AD的延长线于G，AC的延长线交FG于H，连接BG，下列结论：①∠DAE＝∠F；②∠DAE＝(∠ABD﹣∠ACE)；③S△AEB：S△AEC＝AB：AC；④∠AGH＝∠BAE+∠ACB，其中正确的结论有（ ）个．

A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

如图，①根据三角形的内角和即可得到∠DAE＝∠F；②根据角平分线的定义得∠EAC＝，由三角形的内角和定理得∠DAE＝90°﹣∠AED，变形可得结论；③根据三角形的面积公式即可得到S△AEB：S△AEC＝AB：CA；④根据三角形的内角和和外角的性质即刻得到∠AGH＝∠BAE+∠ACB．

解：如图，AE交GF于M，

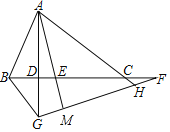
①∵AD⊥BC，FG⊥AE，

∴∠ADE＝∠AMF＝90°，

∵∠AED＝∠MEF，

∴∠DAE＝∠F；故①正确；

②∵AE平分∠BAC交BC于E，

∴∠EAC＝，

∠DAE＝90°﹣∠AED，

＝90°﹣(∠ACE+∠EAC)，

＝90°﹣(∠ACE+)，

＝(180°﹣2∠ACE﹣∠BAC)，

＝ (∠ABD﹣∠ACE)，

故②正确；

③∵AE平分∠BAC交BC于E，

∴点E到AB和AC的距离相等，

∴S△AEB：S△AEC＝AB：CA；故③正确，

④∵∠DAE＝∠F，∠FDG＝∠FME＝90°，

∴∠AGH＝∠MEF，

∵∠MEF＝∠CAE+∠ACB，

∴∠AGH＝∠CAE+∠ACB，

∴∠AGH＝∠BAE+∠ACB；故④正确；

故选：D．