
【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
【答案】(1)补图见解析;(2)甲胜出,理由见解析;(3)见解析.
【解析】
(1)根据折线统计图列举出乙的成绩,计算出甲的中位数,方差,以及乙平均数,中位数及方差,补全即可;
(2)计算出甲乙两人的方差,比较大小即可做出判断;
(3)希望乙胜出,修改规则,使乙获胜的概率大于甲即可.
(1)根据折线统计图得乙的射击成绩为2,4,6,8,7,7,8,9,9,10,
则平均数为![]() (环),中位数为7.5环,
(环),中位数为7.5环,
方差为![]()
![]() .
.
由图和表可得甲的射击成绩为9,6,7,6,2,7,7,8,9,平均数为7环.
则甲第8次成绩为![]() (环).
(环).
所以甲的10次成绩为2,6,6,7,7,7,8,9,9,9,中位数为7环,
方差为![]()
![]() .
.
补全表格如下:
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 4 | 0 |
乙 | 7 | 5.4 | 1 |
甲、乙射击成绩折线统计图
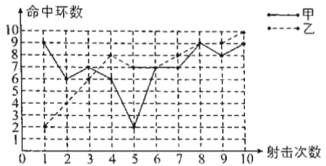
(2)甲应胜出因为甲的方差小于乙的方差,甲的成绩比较稳定,故甲胜出.
(3)制定的规则不唯一,如:如果希望乙胜出,应该制定的评判规则为平均成绩高的胜出;
如果平均成绩相同,则随着比赛的进行,发挥越来越好者或命中满环(10环)次数多者胜出.
因为甲、乙的平均成绩相同,乙只有第5次射击比第4次射击少命中1环,
且命中1次10环,
而甲第2次比第1次第4次比第3次、第5次比第4次、第9次比第8次命中环数都低,
且命中10环的次数为0,
即随着比赛的进行,乙的射击成绩越来越好,
故乙胜出.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.
(1)求抛物线的解析式;
(2)直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;
(3)连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么点A2019的坐标为( )
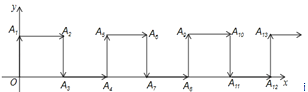
A.(1008,1)B.(1009,1)C.(1009,0)D.(1010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图: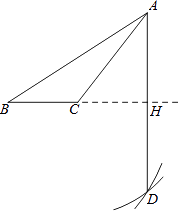
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是 . 他的依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com