
【题目】已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.
(1)求抛物线的解析式;
(2)直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;
(3)连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
【答案】
(1)解:将A(﹣1,0),B(3,0)代入得: ![]() ,
,
解得:b=﹣2,c=﹣3.
抛物线的解析式为y=x2﹣2x﹣3
(2)解:由x=﹣ ![]() 得;抛物线的对称轴为x=1.
得;抛物线的对称轴为x=1.
设点P的坐标为(a,a2﹣2a﹣3).
设直线PA的解析式为y=kx+b.
将点P和点A的坐标代入得: ![]() ,解得:k=a﹣3,b=a﹣3.
,解得:k=a﹣3,b=a﹣3.
∴直线PA的解析式为y=(a﹣3)x+a﹣3.
将x=1代入得:y1=2a﹣6.
设直线PB的解析式为y=k1x+b1.
将点P和点B的坐标代入得: ![]() ,解得:k=a+1,b=﹣3a﹣3.
,解得:k=a+1,b=﹣3a﹣3.
∴直线PB的解析式为y=(a+1)x﹣3a﹣3.
将x=1代入得:y2=﹣2a﹣2.
∴y1+y2=﹣8.
(3)解:如图所示:
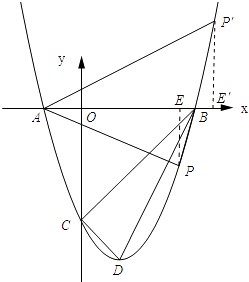
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的顶点坐标为(1,﹣4).
∵将x=0代入抛物线的解析式得;y=﹣3,
∴C(0,﹣3).
由两点间的距离公式可知:BC=3 ![]() ,DC=
,DC= ![]() ,BD=2
,BD=2 ![]() .
.
∵BC2+DC2=BD2,
∴△BCD为直角三角形.
∴tan∠CBD= ![]() =
= ![]() .
.
设点P的坐标为(a,a2﹣2a﹣3).
∵∠PAB=∠CBD,
∴ ![]() =
= ![]() .
.
整理得:a﹣3= ![]() .
.
解得:a=3 ![]() 或a=2
或a=2 ![]() .
.
∴当a=2 ![]() 时,a+1=
时,a+1= ![]() ,则a2﹣2a﹣3=
,则a2﹣2a﹣3= ![]() =﹣
=﹣ ![]() .
.
∴点P的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
当a= ![]() 时,a+1=
时,a+1= ![]() ,则a2﹣2a﹣3=
,则a2﹣2a﹣3= ![]() =
= ![]() .
.
∴点P′的坐标为( ![]() ,
, ![]() ).
).
综上所述,点P的坐标为( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )
)
【解析】(1)用待定系数法,把A(﹣1,0),B(3,0)代入抛物线,求出抛物线的解析式;(2)由抛物线的对称轴为x=1,得到直线PA的解析式和直线PB的解析式,求出y1+y2的值;(3)由抛物线的解析式得到抛物线的顶点坐标,求出C点坐标,根据两点间的距离公式求出BC、DC、BD的值,根据勾股定理的逆定理得到△BCD为直角三角形;根据三角函数值求出点P的坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.


科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形的一锐角α(45°<α<90°)的正弦和余弦分别是方程(m+5)x2﹣(2m﹣5)x+12=0的两根,求:
(1)m的值;
(2)α的正弦值和余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,G是线段AB上一点,AC和DG相交于点E.
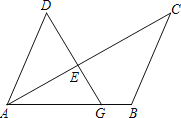
(1)请先作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
(2)然后证明当:AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.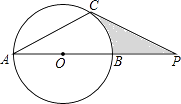
(1)求证:CP是⊙O的切线;
(2)若PC=6,AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将![]() 纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
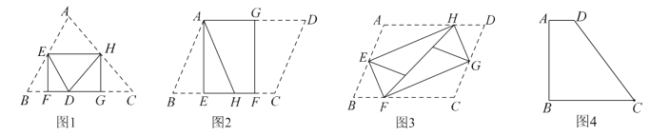
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_______,__________;
,则操作形成的折痕分别是线段_______,__________;![]() ___________.
___________.
(2)将![]() 纸片按图3的方式折叠成一个叠合矩形
纸片按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图4,四边形![]() 纸片满足
纸片满足![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出
,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出![]() 、
、![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.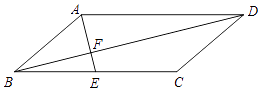
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD= ![]() 时,若CD=
时,若CD= ![]() ,求AD长.
,求AD长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com