
【题目】已知三角形的一锐角α(45°<α<90°)的正弦和余弦分别是方程(m+5)x2﹣(2m﹣5)x+12=0的两根,求:
(1)m的值;
(2)α的正弦值和余弦值.
【答案】(1)20;(2)sinα=![]() ,cosα=
,cosα=![]()
【解析】
(1)设一个直角三角形的两个锐角为∠A、∠B,且∠A+∠B=90°,利用正弦三角公式及完全平方公式得![]() ﹣2sinAsinB=1,列一元二次方程求解即可;
﹣2sinAsinB=1,列一元二次方程求解即可;
(2) 当m=20时,方程转化为(5x﹣3)(5x﹣4)=0,求解即可得到正弦值和余弦值,且注意α为锐角.
解:(1)设一个直角三角形的两个锐角为∠A、∠B(∠A+∠B=90°),
∴sinB=cosA,
根据题意,得:sinA+sinB=![]() ,sinAsinB=
,sinAsinB=![]() ,
,
∵![]() ,
,
∴![]() ﹣2sinAsinB=1,
﹣2sinAsinB=1,
∴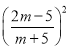 ﹣2×
﹣2×![]() =1,
=1,
解得![]() =20,
=20,![]() =﹣2,
=﹣2,
检验:把![]() =20代入检验是原方程的根,把
=20代入检验是原方程的根,把![]() =﹣2代入检验是原方程的根,
=﹣2代入检验是原方程的根,
∵sinA+sinB=![]() >0,sinAsinB=
>0,sinAsinB=![]() <1,
<1,
∴m=20;
(2)当m=20时,方程转化为(5x﹣3)(5x﹣4)=0,
解得![]() ,
,
∵45°<α<90°,
∴sinα>cosα,
∴sinα=![]() ,cosα=
,cosα=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某班为了准备奖品,王老师购买了笔记本和钢笔共![]() 件,笔记本一本
件,笔记本一本![]() 元,钢笔一支
元,钢笔一支![]() 元,一共
元,一共![]() 元.
元.
(1)笔记本、钢笔各多少件?
(2)王老师计划再购买笔记本和钢笔共![]() 件(钢笔和笔记本每样至少一件),但是两次总花费不得超过
件(钢笔和笔记本每样至少一件),但是两次总花费不得超过![]() 元,有多少种购买方案?请将购买方案一一写出.
元,有多少种购买方案?请将购买方案一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB是直径,∠BCD=120°,∠APD=30°,则∠ADP的度数为( )
A.45°
B.40°
C.35°
D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CD是经过∠BCA定点C的一条直线,CA=CB,E、F分别是直线CD上两点,且∠BEC=∠CFA=∠β.
(1)若直线CD经过∠BCA内部,且E、F在射线CD上,
①若∠BCA=90°,∠β=90°,例如左边图,则BE CF,EF |BE - AF|
(填“>”,“<”,“=”);
②若0°<∠BCA<180°,且∠β+∠BCA=180°,例如中间图,①中的两个结论还成立吗?并说明理由;
(2)如右边图,若直线CD经过∠BCA外部,且∠β=∠BCA,请直接写出线段EF、BE、AF的数量关系(不需要证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.
(1)求抛物线的解析式;
(2)直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;
(3)连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
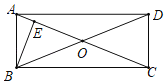
【题目】如图,ABCD的对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:四边形ABCD为矩形;
(2)过B作BE⊥AO于E,∠CBE=3∠ABE,BE=2,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com