
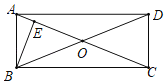
【题目】如图,ABCD的对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:四边形ABCD为矩形;
(2)过B作BE⊥AO于E,∠CBE=3∠ABE,BE=2,求AE的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据等角对等边得出OB=OC,根据平行四边形性质求出OC=OA=![]() AC,OB=OD=
AC,OB=OD=![]() BD,推出AC=BD,根据矩形的判定推出即可.
BD,推出AC=BD,根据矩形的判定推出即可.
(2)根据矩形的性质和∠CBE=3∠ABE,得出∠ABE=22.5°,在EB上取一点H,使得EH=AE,易证AH=BH,设AE=EB=x,则AH=BH=![]() x,构建方程即可解决问题.
x,构建方程即可解决问题.
(1)证明:∵∠OBC=∠OCB,
∴OB=OC,
∵四边形ABCD是平行四边形,
∴OC=OA=![]() AC,OB=OD=
AC,OB=OD=![]() BD,
BD,
∴AC=BD,
∵四边形ABCD是平行四边形,
∴四边形ABCD是矩形;
(2)∵四边形ABCD是矩形,
∴∠ABC=90°,
∵∠CBE=3∠ABE,
∴∠ABE=![]() ×90°=22.5°,
×90°=22.5°,
∵BE⊥AO,
∠BAE=90°-∠ABE=67.5°,
在EB上取一点H,使得EH=AE,
∴∠HAE=∠AHE=45°,
∴∠BAH=∠BAE-∠HAE=22.5°,
∴∠BAH=∠ABE=22.5°,
∴AH=BH,
设AE=EB=x,则AH=BH=![]() =
=![]() x,
x,

∵BE=2,
∴x+![]() x=2,
x=2,
∴x=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知三角形的一锐角α(45°<α<90°)的正弦和余弦分别是方程(m+5)x2﹣(2m﹣5)x+12=0的两根,求:
(1)m的值;
(2)α的正弦值和余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.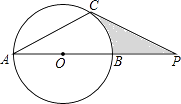
(1)求证:CP是⊙O的切线;
(2)若PC=6,AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将![]() 纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
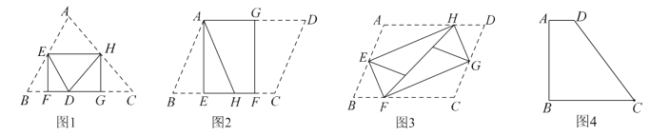
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_______,__________;
,则操作形成的折痕分别是线段_______,__________;![]() ___________.
___________.
(2)将![]() 纸片按图3的方式折叠成一个叠合矩形
纸片按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图4,四边形![]() 纸片满足
纸片满足![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出
,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出![]() 、
、![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建设工地一个工程有大量的沙石需要运输.建设公司车队有载重量为8吨和10吨的卡车共12辆,全部车辆一次能运输110吨沙石
(1)求建设公司车队载重量为8吨和10吨的卡车各有多少辆?
(2)随着工程的进展,车队需要一次运输沙石超过160吨,为了完成任务,准备新增购这两种卡车共6辆,车队最多新购买载重量为8吨的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道三角形任意两条中线的交点是三角形的重心.重心有如下性质:重心到顶点的距离是重心到对边中点距离的2倍.请利用该性质解决问题

(1)如图1,在△ABC中,AF、BE是中线,AF⊥BE于P.若BP=2,∠FAB=30°,则EP= ,FP= ;
(2)如图1,在△ABC中,BC=a,AC=b,AB=c,AF、BE是中线,AF⊥BE于P.猜想a2、b2、c2三者之间的关系并证明;
(3)如图2,在ABCD中,点E、F、G分别是AD、BC、CD的中点,BE⊥BG,AB=3,AD=2![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.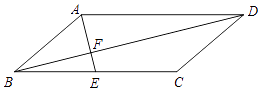
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD= ![]() 时,若CD=
时,若CD= ![]() ,求AD长.
,求AD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。
(1)求购买一个足球、一个篮球各需多少元?
(2)根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com