
【题目】我们知道三角形任意两条中线的交点是三角形的重心.重心有如下性质:重心到顶点的距离是重心到对边中点距离的2倍.请利用该性质解决问题

(1)如图1,在△ABC中,AF、BE是中线,AF⊥BE于P.若BP=2,∠FAB=30°,则EP= ,FP= ;
(2)如图1,在△ABC中,BC=a,AC=b,AB=c,AF、BE是中线,AF⊥BE于P.猜想a2、b2、c2三者之间的关系并证明;
(3)如图2,在ABCD中,点E、F、G分别是AD、BC、CD的中点,BE⊥BG,AB=3,AD=2![]() ,求AF的长.
,求AF的长.
【答案】(1)1,![]() ;(2)a2+b2=5c2,理由见解析;(3)AF=4
;(2)a2+b2=5c2,理由见解析;(3)AF=4
【解析】
(1)由三角形的重心定理得出BP=2EP=2,AP=2FP,得出EP=1,由直角三角形的性质得出AP=![]() BP=2
BP=2![]() ,即可得出FP=
,即可得出FP=![]() AP=
AP=![]() ;
;
(2)设PF=m,PE=n,由 ![]() ,得到AP=2m,PB=2n,再由勾股定理即可得出结论;
,得到AP=2m,PB=2n,再由勾股定理即可得出结论;
(3)连接AC、EC,由平行四边形的性质得出AD=BC,AD∥BC,证明四边形AFCE是平行四边形,得出AF=CE,由平行线得出△AEQ∽△CBQ,得出![]() ,设AQ=a,EQ=b,则CQ=2a,BQ=2b,证明EG是△ACD的中位线,由三角形中位线定理得出EG∥AC,得出BE⊥AC,由勾股定理得得出方程,求出a2=
,设AQ=a,EQ=b,则CQ=2a,BQ=2b,证明EG是△ACD的中位线,由三角形中位线定理得出EG∥AC,得出BE⊥AC,由勾股定理得得出方程,求出a2=![]() ,得出BQ2=4b2=
,得出BQ2=4b2=![]() ,b2=
,b2=![]() ,在Rt△EQC中,由勾股定理求出CE,即可得出AF的长.
,在Rt△EQC中,由勾股定理求出CE,即可得出AF的长.
解:(1)∵在△ABC中,AF、BE是中线,
∴BP=2EP=2,AP=2FP,
∴EP=1,
∵AF⊥BE,∠FAB=30°,
∴AB=2BP=4,
∴AP=![]() ,
,
∴FP=![]() AP=
AP=![]() ;
;
故答案为:1,![]() ;
;
(2)a2+b2=5c2;理由如下:
连接EF,如图1所示:
∵AF,BE是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥AB,且EF=![]() AB=
AB=![]() c,
c,
∴![]() ,
,
设PF=m,PE=n,
∴AP=2m,PB=2n,
在Rt△APB中,(2m)2+(2n)2=c2,即4m2+4n2=c2,
在Rt△APE中,(2m)2+n2=(![]() b)2,即4m2+n2=
b)2,即4m2+n2=![]() b2,
b2,
在Rt△FPB中,m2+(2n)2=(![]() a)2,即m2+4n2=
a)2,即m2+4n2=![]() a2,
a2,
∴5m2+5n2=![]() (a2+b2)=
(a2+b2)=![]() c2,
c2,
∴a2+b2=5c2;
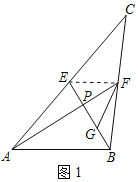
(3)连接AC、EC,如图2所示:
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∵点E,F分别是AD,BC,CD的中点,
∴AE=CE,
∴四边形AFCE是平行四边形,
∴AF=CE,
∵AD∥BC,
∴△AEQ∽△CBQ,
∴![]() ,
,
设AQ=a,EQ=b,则CQ=2a,BQ=2b,
∵点E,G分别是AD,CD的中点,
∴EG是△ACD的中位线,
∴EG∥AC,
∵BE⊥EG,
∴BE⊥AC,
由勾股定理得:AB2﹣AQ2=BC2﹣CQ2,
即9﹣a2=(2![]() )2﹣4a2,
)2﹣4a2,
∴3a2=11,
∴a2=![]() ,
,
∴BQ2=4b2=(2![]() )2﹣4×
)2﹣4×![]() =
=![]() ,
,
∴b2=![]() ×
×![]() =
=![]() ,
,
在Rt△EQC中,CE2=EQ2+CQ2=b2+4a2=16,
∴CE=4,
∴AF=4.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么点A2019的坐标为( )
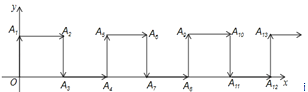
A.(1008,1)B.(1009,1)C.(1009,0)D.(1010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
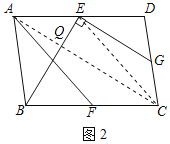
【题目】如图,ABCD的对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:四边形ABCD为矩形;
(2)过B作BE⊥AO于E,∠CBE=3∠ABE,BE=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图: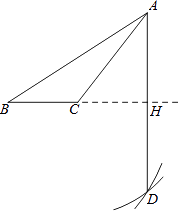
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是 . 他的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货共19吨;用2辆A型车和3辆B型车载满货物一次可运货共21吨.
(1)1辆A型车和1辆B型车都载满货物一次分别可以运货多少吨?
(2)某物流公司现有49吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.
①求![]() 、
、![]() 的值;
的值;
②若A型车每辆需租金130元/次,B型车每辆需租金200元/次.请求出租车费用最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意有理数x,用[x]表示不大于x的最大整数.例如:[1.3]=1,[3]=3,[﹣2.5]=﹣3.以下结论正确的是_____.(把你认为正确结论的序号都填上)
①[﹣3.14]=﹣4;
②﹣[﹣x]=[x];
③[2x]=2[x];
④若[![]() ]=﹣4,则x的取值范围是﹣
]=﹣4,则x的取值范围是﹣![]() ≤x<﹣
≤x<﹣![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com