
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图: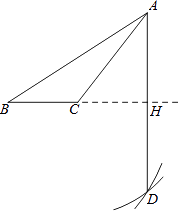
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是 . 他的依据是 .
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两名选手中选拔出一个人参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表.
甲、乙射击成绩统计表
平均数(环) | 中位数(环) | 方差 | 命中10环的次数 |
甲 | 7 | 0 | |
乙 | 1 |
甲、乙射击成绩折线统计图

(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将![]() 纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
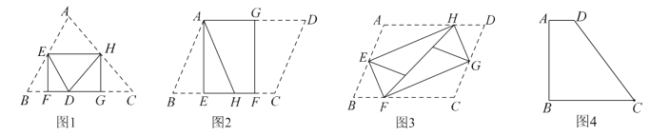
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_______,__________;
,则操作形成的折痕分别是线段_______,__________;![]() ___________.
___________.
(2)将![]() 纸片按图3的方式折叠成一个叠合矩形
纸片按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图4,四边形![]() 纸片满足
纸片满足![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出
,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出![]() 、
、![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道三角形任意两条中线的交点是三角形的重心.重心有如下性质:重心到顶点的距离是重心到对边中点距离的2倍.请利用该性质解决问题

(1)如图1,在△ABC中,AF、BE是中线,AF⊥BE于P.若BP=2,∠FAB=30°,则EP= ,FP= ;
(2)如图1,在△ABC中,BC=a,AC=b,AB=c,AF、BE是中线,AF⊥BE于P.猜想a2、b2、c2三者之间的关系并证明;
(3)如图2,在ABCD中,点E、F、G分别是AD、BC、CD的中点,BE⊥BG,AB=3,AD=2![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.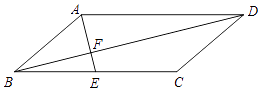
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD= ![]() 时,若CD=
时,若CD= ![]() ,求AD长.
,求AD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y= ![]() 的图象与性质,小静根据学习函数的经验,对函数y=
的图象与性质,小静根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
的图象与性质进行了探究,下面是小静的探究过程,请补充完整: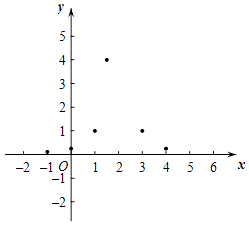
(1)函数y= ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下表是y与x的几组对应值.
x | … | ﹣1 | 0 | 1 |
|
| 3 | 4 | … |
y | … |
|
| 1 | 4 | m | 1 |
| … |
表中的m=;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少? .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com