
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.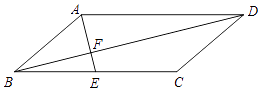
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD= ![]() 时,若CD=
时,若CD= ![]() ,求AD长.
,求AD长.
【答案】
(1)证明:∵四边形ABCD为平行四边形∴AD∥BC,AD=BC,AB=CD,
∵点E为BC的中点,
∴BE= ![]() BC=
BC= ![]() AD,
AD,
∵AD∥BC,
∴△BEF∽△DAF,
∴ ![]() =
= ![]() ,
,
∴DF=2BF
(2)解:∵CD= ![]() ,
,
∴AB=CD= ![]() ,
,
∵在Rt△ABF中,∠AFB=90°,∴tan∠ABD= ![]() =
= ![]() ,
,
∴设AF=x,则BF=2x,
∴AB= ![]() =
= ![]() x=
x= ![]() ,
,
∴x=1,AF=1,BF=2,
∵DF=2BF,
∴DF=4,
∴AD= ![]() =
= ![]()
【解析】(1)由平行四边形的性质的出AD∥BC,AD=BC,AB=CD,再据相似三角形的判定定理得△BEF∽△DAF,最后由相似三角形的对应边成比例得出DF=2BF;(2)由平行四边形的性质对边相等得出AB=CD,再Rt△ABF中由锐角三角函数,及勾股定理得出AD的长度。
【考点精析】利用平行四边形的性质和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.
(1)求抛物线的解析式;
(2)直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;
(3)连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:四边形ABCD为矩形;
(2)过B作BE⊥AO于E,∠CBE=3∠ABE,BE=2,求AE的长.
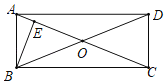
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图: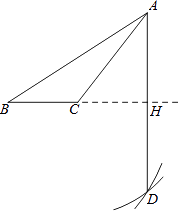
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是 . 他的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的表达式为:
的表达式为:![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 的表达式为
的表达式为![]() ,
,![]() 经过点
经过点![]() ,
,![]() ,
,![]() ,
,![]() 交于点
交于点![]() .
.
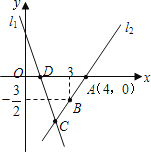
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)直接写出点![]() 的坐标________;
的坐标________;
(3)如果点![]() 在直线
在直线![]() 上,满足
上,满足![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(4)把![]() 向左平移
向左平移![]() 个单位到
个单位到![]() 的位置,当
的位置,当![]() 取得最小值时,直接写出
取得最小值时,直接写出![]() 的值
的值![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货共19吨;用2辆A型车和3辆B型车载满货物一次可运货共21吨.
(1)1辆A型车和1辆B型车都载满货物一次分别可以运货多少吨?
(2)某物流公司现有49吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都载满货物.
辆,一次运完,且恰好每辆车都载满货物.
①求![]() 、
、![]() 的值;
的值;
②若A型车每辆需租金130元/次,B型车每辆需租金200元/次.请求出租车费用最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,中国在线旅游产业发展迅猛,在线旅游产业是依托互联网,以满足旅游消费者信息查询、产品预订及服务评价为核心目的,囊括了包括航空公司、酒店、景区、租车公司、海内外旅游服务供应商及搜索引擎、OTA、电信运营商、旅游资讯及社区网站等在线旅游平台的新产业.
据数据统计:2012年中国在线旅游市场交易金额约为2219亿元,2013年中国在线旅游市场交易金额约为3015亿元,2014年中国在线旅游市场交易金额相比2013年增加了1117亿元,2015年中国在线旅游市场交易金额约为5424亿元,2016年中国在线旅游市场交易金额为6622亿元,在人们对休闲旅游观念的不断加强之下,未来两年中国在线旅游市场交易规模会持续上涨.
(1)请用折线统计图或条形统计图将2012﹣2016年中国在线旅游市场交易金额的数据描述出来,并在图中标明相应数据;
(2)根据绘制的统计图中提供的信息,预估2017年中国在线旅游市场交易金额约为亿元,你的预估理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0),B(b,3),C(4,0),且满足(a+b)2+|a﹣b+6|=0,线段AB交y轴于F点.
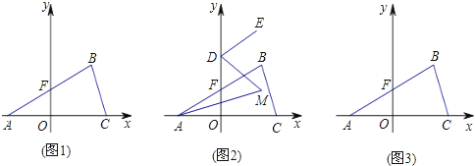
(1)求点A、B的坐标.
(2)点D为y轴正半轴上一点,若ED∥AB,且AM,DM分别平分∠CAB,∠ODE,如图2,求∠AMD的度数.
(3)如图3,
①求点F的坐标;
②点P为坐标轴上一点,若△ABP的三角形和△ABC的面积相等?若存在,求出P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com