
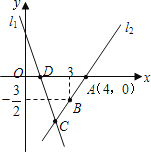
【题目】如图,直线![]() 的表达式为:
的表达式为:![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 的表达式为
的表达式为![]() ,
,![]() 经过点
经过点![]() ,
,![]() ,
,![]() ,
,![]() 交于点
交于点![]() .
.
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)直接写出点![]() 的坐标________;
的坐标________;
(3)如果点![]() 在直线
在直线![]() 上,满足
上,满足![]() 的面积是
的面积是![]() 面积的2倍,求点
面积的2倍,求点![]() 的坐标;
的坐标;
(4)把![]() 向左平移
向左平移![]() 个单位到
个单位到![]() 的位置,当
的位置,当![]() 取得最小值时,直接写出
取得最小值时,直接写出![]() 的值
的值![]() ________.
________.
【答案】(1)y=![]() x6;(2)(2,3);(3)(6,3)或(2,3);(4)
x6;(2)(2,3);(3)(6,3)或(2,3);(4)![]()
【解析】
(1)根据待定系数法可求直线l2的表达式;
(2)联立直线l1与l2的表达式,解方程组即可得到结论;
(3)根据直线l1的解析式y=-3x+3求得D(1,0),设P(m,![]() m-6),根据S△ADP=2S△ADB,列方程即可得到结论;
m-6),根据S△ADP=2S△ADB,列方程即可得到结论;
(4)“把![]() 向左平移
向左平移![]() 个单位到
个单位到![]() 的位置,使
的位置,使![]() 取得最小值”等价为“
取得最小值”等价为“![]() 不动,点E沿直线y=3向右移动m个单位,使
不动,点E沿直线y=3向右移动m个单位,使![]() 取得最小值”,求出点A关于直线y=3的对称点A′的坐标,从而求出直线A′D的解析式,进而求出E′的坐标,即可求解.
取得最小值”,求出点A关于直线y=3的对称点A′的坐标,从而求出直线A′D的解析式,进而求出E′的坐标,即可求解.
(1)设直线l2的表达式为:y=kx+b,
∵直线l2经过点A(4,0),B(3,![]() ),
),
∴ ,解得:
,解得: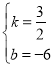 ,
,
∴直线l2的表达式为:y=![]() x6;
x6;
(2)联立可得方程组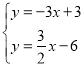 ,解得:
,解得: ![]() ,
,
∴C(2,3),
故答案是:(2,3);
(3)∵直线l1:y=3x+3与x轴交于点D,
∴D(1,0),
∵点![]() 在直线
在直线![]() 上,
上,
∴设P(m,![]() m6),
m6),
∵S△ADP=2S△ADB,
∴![]() ×3|
×3|![]() m6|=2×
m6|=2×![]() ×3×
×3×![]() ,
,
∴m=6或2,
∴点P的坐标(6,3)或(2,3);
(4)由题意得:E(0,3),
“把![]() 向左平移
向左平移![]() 个单位到
个单位到![]() 的位置,
的位置,![]() 取得最小值”等价为“
取得最小值”等价为“![]() 不动,点E沿直线y=3向右移动m个单位,
不动,点E沿直线y=3向右移动m个单位,![]() 取得最小值”,
取得最小值”,
作点A关于直线y=3的对称点A′,连接A′D,交直线y=3于点E′,此时,![]() 取得最小值,
取得最小值,
∵A(4,0),
∴A′(4,6),
设直线A′D的解析式为:y=kx+b,
把A′(4,6),D(1,0)代入得:![]() ,解得:
,解得:![]() ,
,
∴直线A′D的解析式为:y=2x-2,
令y=3代入y=2x-2,解得:x=![]() ,即:E′(
,即:E′(![]() ,3),
,3),
∴m=![]() -0=
-0=![]() .
.
故答案是:![]() .
.



 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建设工地一个工程有大量的沙石需要运输.建设公司车队有载重量为8吨和10吨的卡车共12辆,全部车辆一次能运输110吨沙石
(1)求建设公司车队载重量为8吨和10吨的卡车各有多少辆?
(2)随着工程的进展,车队需要一次运输沙石超过160吨,为了完成任务,准备新增购这两种卡车共6辆,车队最多新购买载重量为8吨的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的一动点(不与点
上的一动点(不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学测验,抽取部分同学的成绩(得分为整数),整理制成如图直方图,根据图示信息描述正确的是( )
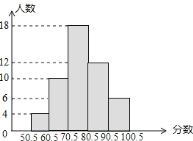
A.抽样的学生共60人
B.60.5~70.5这一分数段的频数为12
C.估计这次测试的及格率(60分为及格)在92%左右
D.估计优秀率(80分以上为优秀)在32%左右
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E为BC的中点,AE与对角线BD交于点F.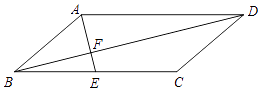
(1)求证:DF=2BF;
(2)当∠AFB=90°且tan∠ABD= ![]() 时,若CD=
时,若CD= ![]() ,求AD长.
,求AD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )

A. 乙先出发的时间为0.5小时 B. 甲的速度是80千米/小时
C. 甲出发0.5小时后两车相遇 D. 甲到B地比乙到A地早![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠A=90°,AB=AC,∠ABC 的角平分线交 AC 于 D,BD=4 ![]() ,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )
,过点 C作 CE⊥BD 交 BD 的延长线于 E,则 CE 的长为( )

A.![]() B.2
B.2 ![]() C.3
C.3 ![]() D.2
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com