[题目]下列美丽的图案.既是轴对称图形又是中心对称图形的个数是( )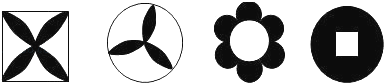A.1个B.2个C.3个D.4个题目和参考答案——青夏教育精英家教网—

【题目】下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（）
A.1个
B.2个
C.3个
D.4个

【答案】C
【解析】根据轴对称图形和中心对称图形的定义的特点，依次判断，可知第一、三、四幅图形即是轴对称图形又是中心对称图形；第二幅图只是轴对称图形，不是中心对称图形。
所以答案是：C.
【考点精析】解答此题的关键在于理解轴对称图形的相关知识，掌握两个完全一样的图形关于某条直线对折，如果两边能够完全重合，我们就说这两个图形成轴对称，这条直线就对称轴，以及对中心对称及中心对称图形的理解，了解如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称；如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图1，将纸片折叠，折叠后的三个三角形可拼合形成一个矩形，类似地，对多边形进行折叠，若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．

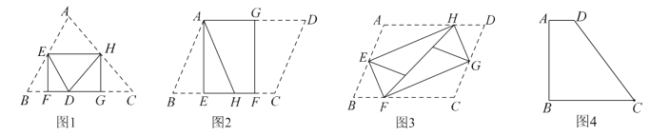
（1）将纸片按图2的方式折叠成一个叠合矩形，则操作形成的折痕分别是线段_______，__________；___________．

（2）将纸片按图3的方式折叠成一个叠合矩形，若，，求的长；

（3）如图4，四边形纸片满足，，，，，小明把该纸片折叠，得到叠合正方形，请你帮助画出一种叠合正方形的示意图，并求出、的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平行四边形ABCD中，点E为BC的中点，AE与对角线BD交于点F．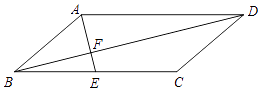

（1）求证：DF=2BF；
（2）当∠AFB=90°且tan∠ABD= 时，若CD= ，求AD长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】有这样一个问题：探究函数y= 的图象与性质，小静根据学习函数的经验，对函数y= 的图象与性质进行了探究，下面是小静的探究过程，请补充完整：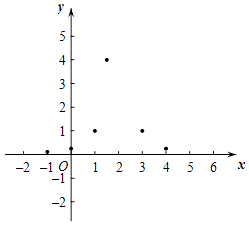

（1）函数y= 的自变量x的取值范围是；
（2）下表是y与x的几组对应值．

x	…	﹣1	0	1			3	4	…
y	…			1	4	m	1		…

表中的m=；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；
（4）结合函数图象，写出一条该函数图象的性质：．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为了更好的治理西流湖水质，保护环境，市治污公司决定购买 10 台污水处理设备．现有 A、B 两种型号的设备，其中每台的价格，月处理污水量如下表：

	A 型	B 型
价格（万元/台）	a	b
处理污水量（吨／月）	240	200

经调查：购买一台 A 型设备比购买一台 B 型设备多 2 万元，购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元．

（1）求 a，b 的值；

（2）经预算：市治污公司购买污水处理设备的资金不超过 105 万元，你认为该公司有哪几种购买方案；

（3）在（2）问的条件下，若每月要求处理西流湖的污水量不低于 2040 吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系中，已知抛物线与直线的图象如图所示，当y1≠y2时，取y1 ， y2中的较大值记为N；当y1=y2时，N=y1=y2 ．则下列说法：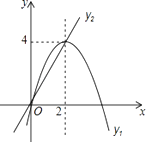
①当0＜x＜2时，N=y1；
②N随x的增大而增大的取值范围是x＜0；
③取y1 ， y2中的较小值记为M，则使得M大于4的x值不存在；
④若N=2，则x=2﹣ 或x=1．
其中正确的有（）
A.1个
B.2个
C.3个
D.4个