
【题目】如图1,将![]() 纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
纸片折叠,折叠后的三个三角形可拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
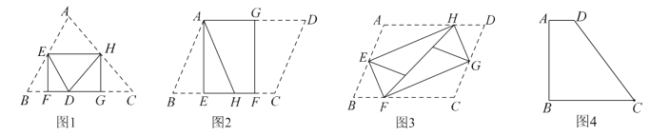
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_______,__________;
,则操作形成的折痕分别是线段_______,__________;![]() ___________.
___________.
(2)将![]() 纸片按图3的方式折叠成一个叠合矩形
纸片按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图4,四边形![]() 纸片满足
纸片满足![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出
,小明把该纸片折叠,得到叠合正方形,请你帮助画出一种叠合正方形的示意图,并求出![]() 、
、![]() 的长.
的长.
【答案】(1)AE,GF,1:2;(2)13;(3)AD =1,BC =7;
【解析】
(1)根据题意得出操作形成的折痕分别是线段AE、GF;由折叠的性质得出△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,得出S矩形AEFG=![]() SABCD,即可得出答案;
SABCD,即可得出答案;
(2)由矩形的性质和勾股定理求出FH,即可得出答案;
(3)由折叠的性质得:AD=BG,AE=BE=![]() AB=4,CF=DF=
AB=4,CF=DF=![]() CD=5,GM=CM,∠FMC=90°,由叠合正方形的性质得出BM=FM=4,由勾股定理得出GM=CM=
CD=5,GM=CM,∠FMC=90°,由叠合正方形的性质得出BM=FM=4,由勾股定理得出GM=CM=![]() =3,得出AD=BG=BM-GM=1,BC=BM+CM=7;
=3,得出AD=BG=BM-GM=1,BC=BM+CM=7;
解:(1)根据题意得:操作形成的折痕分别是线段AE、GF;
由折叠的性质得:△ABE≌△AHE,四边形AHFG≌四边形DCFG,
∴△ABE的面积=△AHE的面积,四边形AHFG的面积=四边形DCFG的面积,
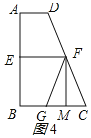
∴S矩形AEFG=![]() SABCD,
SABCD,
∴S矩形AEFG:SABCD=1:2;
故答案为:AE,GF,1:2;
(2)∵四边形EFGH是矩形,
∴∠HEF=90°,
∴FH=![]() =13,
=13,
由折叠的性质得:AD=FH=13;
(3)图5所示:
如图4所示:由折叠的性质得:AD=BG,AE=BE=![]() AB=4,CF=DF=
AB=4,CF=DF=![]() CD=5,GM=CM,∠FMC=90°,
CD=5,GM=CM,∠FMC=90°,
∵四边形EFMB是叠合正方形,
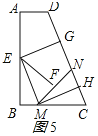
∴BM=FM=4,
∴GM=CM=![]() =3,
=3,
∴AD=BG=BM-GM=1,BC=BM+CM=7;


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b,c 为常数)与x轴交于点A(﹣1,0),点 B(3,0),与y轴交于点C,其顶点为D,点P(不与点 A,B 重合)为抛物线上的一个动点.
(1)求抛物线的解析式;
(2)直线PA,PB分别于抛物线的对称轴交于M,N 两点,设M,N 两点的纵坐标分别为y1 , y2 , 求y1+y2的值;
(3)连接BC,BD,当∠PAB=∠CBD时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),……,那么点A2019的坐标为( )
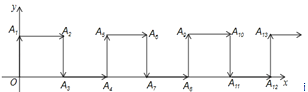
A.(1008,1)B.(1009,1)C.(1009,0)D.(1010,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A,B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
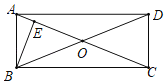
【题目】如图,ABCD的对角线AC、BD相交于点O,且∠OBC=∠OCB.
(1)求证:四边形ABCD为矩形;
(2)过B作BE⊥AO于E,∠CBE=3∠ABE,BE=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角△ABC,老师按照如下步骤尺规作图: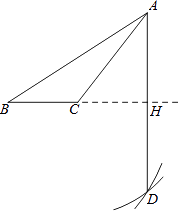
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
小明说:图中的BH⊥AD且平分AD.
小丽说:图中AC平分∠BAD.
小强说:图中点C为BH的中点.
他们的说法中正确的是 . 他的依据是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com