
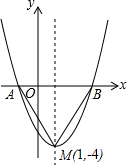
 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)分析 (1)根据抛物线的顶点坐标可以得到抛物线解析式,结合解析式写出抛物线的开口方向和对称轴;
(2)结合抛物线图象回答问题;
(3)由条件可先求得二次函数的解析式,再令y=0可求得A、B两点的坐标;
(4)由条件可先求得P点的纵坐标,再代入解析式可求得P点坐标.
解答 解:(1)∵抛物线解析式为y=(x+m)2+k的顶点为M(1,-4)
∴y=(x-1)2-4,抛物线对称轴是x=1.
∵a=1>0,
∴抛物线开口方向向上.
(2)∵抛物线顶点坐标为M(1,-4),开口方向向上,
∴函数y有最小值,最小值是-4;
(3)∵抛物线解析式为y=(x-1)2-4,令y=0得(x-1)2-4=0解得x1=3,x2=-1
∴A(-1,0),B(3,0);
(2)∵△PAB与△MAB同底,且S△PAB=$\frac{5}{4}$S△MAB,
∴|yP|=$\frac{5}{4}$|yM|=$\frac{5}{4}$×4-5,即yP=±5
又∵点P在y=(x-1)2-4的图象上,yP≥-4,
∴yP=5,则(x-1)2-4=5,
解得x1=4,x2=-2
∴存在合适的点P,坐标为(4,5)或(-2,5).
点评 本题主要考查二次函数综合题,其中需要掌握待定系数法求函数解析式及二次函数图象点点的坐标,掌握二次函数顶点式y=a(x-h)2+k的顶点坐标为(h,k)是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 开口向下 | B. | 对称轴为x=3 | ||
| C. | 顶点坐标为(-3,2) | D. | 当x≥3时,y随x增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
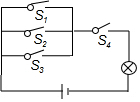 如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )
如图,随机闭合开关S1、S2、S3、S4中的两个,则灯泡发光的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
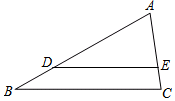 如图,在△ABC中,点D、E分别在AB、AC边上,且DE∥BC,若AD:DB=3:1,AE=6,则AC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,且DE∥BC,若AD:DB=3:1,AE=6,则AC等于( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
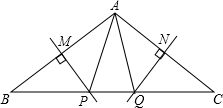 如图所示,MP和 NQ分别垂直平分AB 和AC.
如图所示,MP和 NQ分别垂直平分AB 和AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com