
分析 (1)根据有理数的加法和减法可以解答本题;
(2)根据有理数的加法和减法可以解答本题;
(3)根据有理数的加法和减法可以解答本题;
(4)根据有理数的加法和减法、乘法可以解答本题.
解答 解:(1)3-(+63)-(-259)-(-41)
=3+(-63)+259+41
=240;
(2)(+2$\frac{1}{3}$)-(+10$\frac{1}{3}$)+(-8$\frac{1}{5}$)-(+3$\frac{2}{5}$)
=2$\frac{1}{3}$+(-10$\frac{1}{3}$)+(-8$\frac{1}{5}$)+(-3$\frac{2}{5}$)
=-19$\frac{3}{5}$;
(3)(+4.3)-(-4)+(-2.3)-(+4)
=4.3+4+(-2.3)+(-4)
=2;
(4)-4-2×32+(-2×32)
=-4-64-64
=-124.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
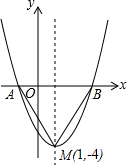 如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)
如图是二次函数y=(x+m)2+k的图象,其顶点坐标为M(1,-4),抛物线与x轴的交点为A、B(点A在点B的左边)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
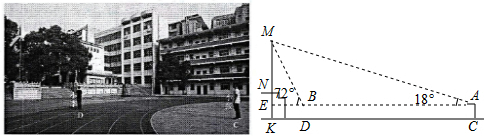
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a>0,b>0,则a+b>0 | B. | 若a<0,b<0,则a-b<0 | ||
| C. | 若a>0,b<0,且|a|>|b|,则a-b>0 | D. | 若a<0,b>0,且|a|>|b|,则a-b<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
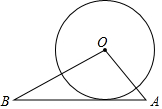 如图,在△OAB中,OA=2$\sqrt{5}$,OB=4$\sqrt{5}$,OA⊥OB,以O为圆心,4为半径作⊙O,求证:AB是⊙O的切线.
如图,在△OAB中,OA=2$\sqrt{5}$,OB=4$\sqrt{5}$,OA⊥OB,以O为圆心,4为半径作⊙O,求证:AB是⊙O的切线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
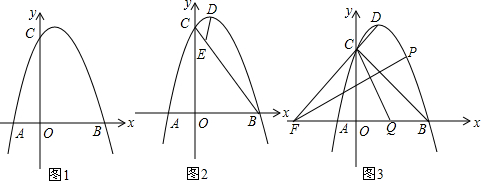
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com