
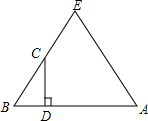
 如图,△ABC是等边三角形,C为BE的中点,CD⊥AB于D,求$\frac{BD}{AD}$的值.
如图,△ABC是等边三角形,C为BE的中点,CD⊥AB于D,求$\frac{BD}{AD}$的值. 分析 作EF⊥AB于F,根据等边三角形的性质得出BF=AF=$\frac{1}{2}$AB,进而证得CD∥EF,由C为BE的中点,证得BD=DF=$\frac{1}{2}$BF=$\frac{1}{4}$AB,得出AD=DF+AF=$\frac{3}{4}$AB,计算$\frac{BD}{AD}$即可求得.
解答 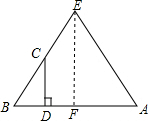 解:作EF⊥AB于F,
解:作EF⊥AB于F,
∵△ABC是等边三角形,
∴BF=AF=$\frac{1}{2}$AB,
∵CD⊥AB,EF⊥AB,
∴CD∥EF,
∵C为BE的中点,
∴D是BF的中点,
∴BD=DF=$\frac{1}{2}$BF=$\frac{1}{4}$AB,
∴AD=DF+AF=$\frac{3}{4}$AB,
∴$\frac{BD}{AD}$=$\frac{1}{3}$.
点评 本题考查了等边三角形的性质和三角形的中位线的性质,作出辅助线构建平行线是解题的关键.


科目:初中数学 来源: 题型:选择题
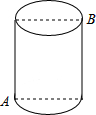 如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
如图,一圆柱高8cm,底面半径为$\frac{6}{π}$ cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
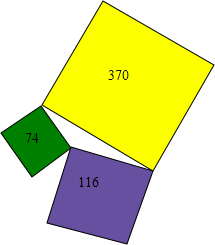 如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少?
如图,一个三角形的湖被三块正方形的土地所包围,这三块正方形土地的面积分别是370英亩、116英亩和74英亩,问:这个三角形湖的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
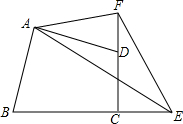 已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.
已知:四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E是BC的延长线上一点,F是CD的延长线上一点,∠BAD=2∠EAF,连结EF.求证:EF=BE-DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
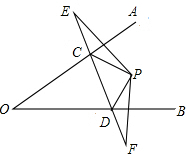 如图,∠A0B内有一点P,分别作出点P关于直线OA,OB的对称点E,F,连接EF交OA于C.交OB于D,已知EF=10cm.求△PCD的周长.
如图,∠A0B内有一点P,分别作出点P关于直线OA,OB的对称点E,F,连接EF交OA于C.交OB于D,已知EF=10cm.求△PCD的周长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8cm | B. | 64cm | C. | 8cm2 | D. | 64cm2 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校八年级3月月考数学试卷(解析版) 题型:单选题
如图,等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
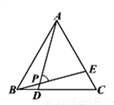
A. 45° B.  60° C. 55° D. 75°
60° C. 55° D. 75°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com