
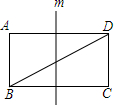
 如图,直线m是矩形ABCD的一条对称轴,∠ADB=30°,点P是直线m上一点,且使得△PAB和△PAD均为等腰三角形,则满足条件的点P共有( )
如图,直线m是矩形ABCD的一条对称轴,∠ADB=30°,点P是直线m上一点,且使得△PAB和△PAD均为等腰三角形,则满足条件的点P共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据线段垂直平分线的性质可得△PAD为等腰三角形,△PAB为等腰三角形,有三种可能:AP=AB或BP=BA或PA=PB.若AP=AB,则点P在以点A为圆心,AB
为半径的圆与直线m的交点处;若BP=BA,则点P在以点B为圆心,BA为半径的圆与直线m的交点处;若PA=PB,则点P在AB的垂直平分线与直线m的交点处.
画出图象,就可解决问题.
解答 解:∵直线m是矩形ABCD的一条对称轴,点P是直线m上一点,
∴PA=PC,∠A=90°,
∴△PAD为等腰三角形.
∵∠ADB=30°,
∴∠ABD=60°.
∵△PAB为等腰三角形,
∴AP=AB或BP=BA或PA=PB.
如图所示,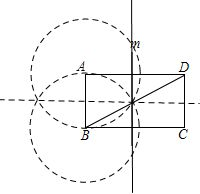
由图可知:满足条件的点P共有3个.
故选C.
点评 本题主要考查了等腰三角形的判定、线段垂直平分线的性质等知识,需要注意的是等腰△PAB并没有指明哪个是腰,需分三种情况讨论,在数满足条件的点的个数时,要考虑有没有重合的现象.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每周做家务的时间(小时) | 0 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 人数(人) | 2 | 2 | 6 | 8 | 12 | 13 | 4 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com