
【题目】如图,正方形ABCD中,E为BC上一点,BE=2CE,连接DE,F为DE中点,以DF为直角边作等腰Rt△DFG,连接BG,将△DFG绕点D顺时针旋转得△DF′G′,G′恰好落在BG的延长线上,连接F′G,若BG=2 ![]() ,则S△GF′G′= .
,则S△GF′G′= . 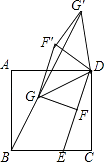
【答案】![]()
【解析】解:如图,作GM⊥BC于M,MG的延长线交AD于N,作DK⊥BG′于K,作KQ⊥DG′于Q,作F′H′BG′于H,BG′交AD于P.
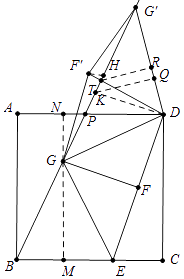
∵BE=2EC,设EC=a,则BE=2a,BC=CD=MN=3a,
∵DG=GE,∠DGE=90°,易证△DGN≌△GEM,设EM=x,
则GN=EM=x,GM=DN=CM=a+x,
∴x+x+a=3a,
∴x=a,
∴BM=EM,∵GM⊥BE,
∴GB=GE=2 ![]() ,
,
∵GM=2a.EM=a,
在Rt△GEM中,可得5a2=20,
∵a>0,
∴a=2,
∴AB=BC=CD=AD=6,GM=4,CM=DN=4,AN=GN=2,DF=EF=GF=G′F′= ![]() ,DG=GE=DG′=2
,DG=GE=DG′=2 ![]() ,
,
∵△GBM∽△BPA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AP=PD=3,
由△APB∽△KPD,可得DK= ![]() ,
,
∵DG′=DG,DK⊥GG′,
∴G′K=GK= ![]() =
= ![]() ,
,
设BG′交DF′于T,作TR⊥DG′于R,
∵tan∠TG′R= ![]() =
= ![]() =
= ![]() ,设TR=3k,RG′=4k,
,设TR=3k,RG′=4k,
∵∠TDR=45°,
∴TR=DR=3k,
∴7k=2 ![]() ,
,
∴k= ![]() ,
,
∴TG′=5k= ![]() ,
,
由△′F′H∽△G′TF′,
可得G′H= ![]() ,
,
在Rt△G′F′H中,F′H= ![]() =
= ![]() ,
,
∴S△GG′F′= ![]() GG′F′H=
GG′F′H= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】关于本题考查的等腰直角三角形和勾股定理的概念,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
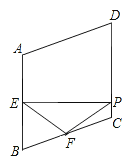
A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1 , 使∠D1AC=60°;连接AC1 , 再以AC1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为 . 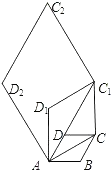
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() .
.![]() 这两直线之间一点.
这两直线之间一点.
(1)如图1,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

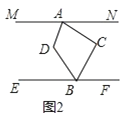
(2)如图2,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并证明你的结论.
有何数量关系?并证明你的结论.
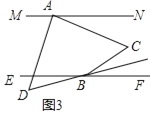
(3)如图3,若![]() 的平分线与
的平分线与![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是__________,依次继续下去……第2 016次输出的结果是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完![]() 假设每分钟的进水量和出水量是两个常数,容器内的水量
假设每分钟的进水量和出水量是两个常数,容器内的水量![]() (单位:升)与时间
(单位:升)与时间![]() (单位:分钟)之间的部分关系如图象所示
(单位:分钟)之间的部分关系如图象所示![]() 从开始进水到把水放完需要多少分钟.( )
从开始进水到把水放完需要多少分钟.( )

A.20B.24C.18D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.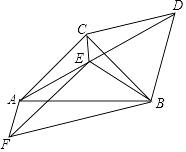
(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°
(1)求tan∠OAB的值;
(2)求图中阴影部分的面积S;
(3)在⊙O上一点P从A点出发,沿逆时针方向运动一周,回到点A,在点P的运动过程中,满足S△POA=S△AOB时,直接写出P点所经过的弧长(不考虑点P与点B重合的情形).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com