
【题目】如图,已知直线![]() .
.![]() 这两直线之间一点.
这两直线之间一点.
(1)如图1,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

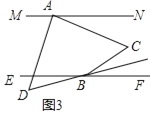
(2)如图2,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并证明你的结论.
有何数量关系?并证明你的结论.
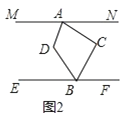
(3)如图3,若![]() 的平分线与
的平分线与![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)∠ADB=50°;(2)∠ADB=180°-![]() ∠ACB,证明见解析;(3)∠ADB=90°-
∠ACB,证明见解析;(3)∠ADB=90°-![]() ∠ACB.
∠ACB.
【解析】
(1)如图1,根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG,根据角平分线的定义得到![]() ,即可得到结论;
,即可得到结论;
(2)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据角平分线的定义得到![]() ,根据平角的定义即可得到结论;
,根据平角的定义即可得到结论;
(3)根据平行线的性质得到∠1=∠ADH,∠2=∠BDH,∠NAC=∠ACG,∠FBC=∠BCG,根据平行线的定义得到![]() ,根据四边形的内角和和角的和差即可得到结论.
,根据四边形的内角和和角的和差即可得到结论.
(1)如图1,过C作CG∥MN,DH∥MN,
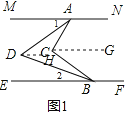
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠MAC=∠ACG,∠EBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴![]() ,
,
∴![]() ;
;
∵∠ACB=100°,
∴∠ADB=50°;
(2)如图2,过C作CG∥MN,DH∥MN,
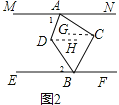
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠BDH,
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠EBC的平分线相交于点D,
∴![]()
∴![]()
![]()
![]() ,
,
∴![]() ;
;
(3)如图3,过C作CG∥MN,DH∥MN,
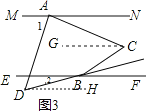
∵MN∥EF,
∴MN∥CG∥DH∥EF,
∴∠1=∠ADH,∠2=∠
∠NAC=∠ACG,∠FBC=∠BCG,
∵∠MAC与∠FBC的平分线相交于点D,
∴![]()
∵![]()
![]()
![]()
![]() .
.
∴![]()


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】一股民在上星期五买进某公司股票1000股,每股27元,下表为本星期内每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股多少元?
星期三收盘时,每股多少元?
![]() 本星期内每股最低价多少元?
本星期内每股最低价多少元?
![]() 本周星期几抛售,获利最大,最大是多少?
本周星期几抛售,获利最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
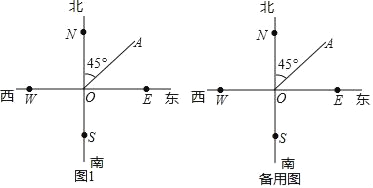
【题目】如图,射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向,点A在点O的北偏东45°方向,点B在点O的北偏西30°方向.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图1或备用图中画出∠BOC;
(2)若OP是∠AOC的角平分线,直接写出∠AOP的度数(不需要计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.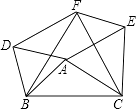
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我校某班同学随机抽取的我国100座城市2017年某天当地pm2.5值的情况的条形统计图,那么本次调查中,PM2.5值的中位数为微克/立方米.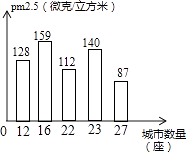
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
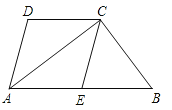
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为BC上一点,BE=2CE,连接DE,F为DE中点,以DF为直角边作等腰Rt△DFG,连接BG,将△DFG绕点D顺时针旋转得△DF′G′,G′恰好落在BG的延长线上,连接F′G,若BG=2 ![]() ,则S△GF′G′= .
,则S△GF′G′= . 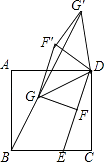
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对我校七年级(1)班喜欢什么球类运动的调查,下列图形中的左图是小明对所调查结果的条形统计图.

(1)问七年级(1)班共有多少学生?
(2)请你改用扇形统计图来表示我校七年级(1)班同学喜欢的球类运动.
(3)从统计图中你可以获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]()
(1)当![]() 所放位置如图①所示时,则
所放位置如图①所示时,则![]() 与
与![]() 的数量关系为_______;请说明理由.
的数量关系为_______;请说明理由.
(2)当![]() 所放位置如图②所示时,
所放位置如图②所示时,![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(3)在(2)的条件下,若![]() 与
与![]() 交于点0,且
交于点0,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
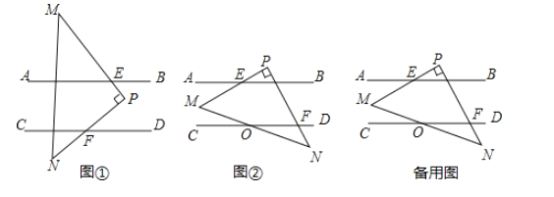
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com