
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
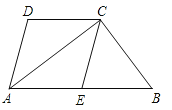
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
【答案】证明:
(1)∵AB∥CD,即AE∥CD,
又∵CE∥AD,∴四边形AECD是平行四边形. 2分
∵AC平分∠BAD,∴∠CAE=∠CAD,
又∵AD∥CE,∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
∴四边形AECD是菱形;········· 4分
(2)证法一:∵E是AB中点,∴AE=BE.
又∵AE=CE,∴BE=CE,∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180°,
∴2∠BCE+2∠ACE=180°,∴∠BCE+∠ACE=90°.
即∠ACB=90°,∴△ABC是直角三角形.
证法二:连DE,则DE⊥AC,且平分AC,
设DE交AC于F,∵E是AB的中点,∴EF∥BC.
∴BC⊥AC,∴△ABC是直角三角形.······· 8分
【解析】
试题(1)先根据平行四边形的定义证得四边形AECD是平行四边形,根据平行线的性质可得∠ACE=∠CAD,再结合角平分线的性质可得AE=CE,从而证得结论;(2)由AE=CE,AE=BE可得BE=CE,即可得到∠B=∠BCE,由∠B+∠BCA+∠BAC=180可得2∠BCE+2∠ACE=180,即可得到结果.
(1)∵AB∥CD, CE∥AD,
∴四边形AECD是平行四边形.
∵CE∥AD,
∴∠ACE=∠CAD.
∵AC平分∠BAD,
∴∠CAE=∠CAD.
∴∠ACE=∠CAE,
∴AE=CE.
∴四边形AECD是菱形;
(2)∵AE=CE,AE=BE,
∴BE=CE,
∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180,
∴2∠BCE+2∠ACE=180,
∴∠BCE+∠ACE=90,即∠ACB=90.
∴△ABC是直角三角形.


科目:初中数学 来源: 题型:
【题目】如图1,在△OAB中,∠OAB=90,∠AOB=30,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
【1】求点B的坐标
【2】求证:四边形ABCE是平行四边形;
【3】如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.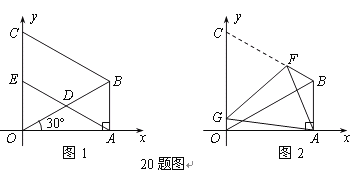
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为![]() ,1,2
,1,2![]() ,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
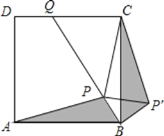
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,
点,![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,
(1)若![]() 点在线段
点在线段![]() (
(![]() 、
、![]() 两点除外)上运动,问
两点除外)上运动,问![]() ,
,![]() ,
,![]() 之间的关系是什么?这种关系是否变化?
之间的关系是什么?这种关系是否变化?
(2)若![]() 点在线段
点在线段![]() 之外时,
之外时,![]() ,
,![]() ,
,![]() 之间的关系怎样?说明理由
之间的关系怎样?说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
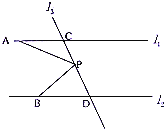
【题目】如图,已知直线![]() .
.![]() 这两直线之间一点.
这两直线之间一点.
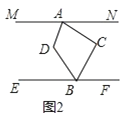
(1)如图1,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

(2)如图2,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并证明你的结论.
有何数量关系?并证明你的结论.
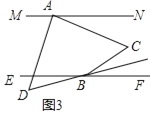
(3)如图3,若![]() 的平分线与
的平分线与![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
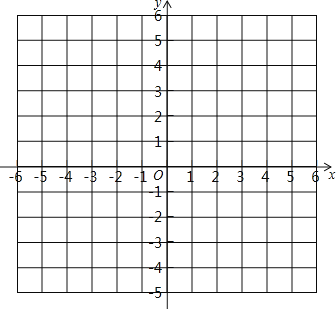
【题目】已知在平面直角坐标系中有三点![]() 、
、![]() 、
、![]() ,请回答如下问题:
,请回答如下问题:
(1)在坐标系内描出点![]() 的位置:
的位置:
(2)求出以![]() 三点为顶点的三角形的面积;
三点为顶点的三角形的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10,若存在,请直接写出点
三点为顶点的三角形的面积为10,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() 的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE=
的图象相交于A、B两点,以AB为边,在直线AB的左侧作菱形ABCD,边BC⊥y轴于点E,若点A坐标为(m,6),tan∠BOE= ![]() ,OE=
,OE= ![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农业观光园将一块面积为![]() 的观光园分成
的观光园分成![]() 三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲
三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株.已知
株.已知![]() 区域的面积是
区域的面积是![]() 的
的![]() 倍,记A区域的面积为
倍,记A区域的面积为![]() 区域的面积为
区域的面积为![]() .
.
花卉 项目 | 甲 | 乙 | 丙 |
面积 |
|
| |
株/ |
|
|
|
数量 |
|
(1)完成上表(结果用含![]() 的代数式表示).
的代数式表示).
(2)若三种花卉共栽种![]() 株
株
①求![]() 与
与![]() 的值.
的值.
②若三种花卉的单价(都是整数)之和为![]() 元,全部栽种共需
元,全部栽种共需![]() 元,求种植面积最大的花卉总价.
元,求种植面积最大的花卉总价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com