
【题目】如图1,在△OAB中,∠OAB=90,∠AOB=30,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
【1】求点B的坐标
【2】求证:四边形ABCE是平行四边形;
【3】如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.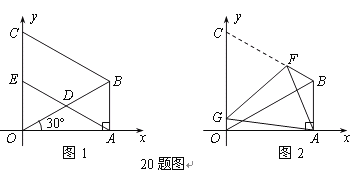
【答案】
【1】 ∵在△OAB中,∠OAB=90,∠AOB=30,OB=8,
∴OA=4![]() ,AB=4。∴点B的坐标为(4
,AB=4。∴点B的坐标为(4![]() ,4)。………2分
,4)。………2分
【2】 ∵∠OAB=90,∴AB⊥![]() 轴,∴AB∥EC。 又∵△OBC是等边三角形,∴OC=OB=8。
轴,∴AB∥EC。 又∵△OBC是等边三角形,∴OC=OB=8。
又∵D是OB的中点,即AD是Rt△OAB斜边上的中线,
∴AD=OD,∴∠OAD=∠AOD=30,∴OE=4。∴EC=OC-OE=4。
∴AB=EC。∴四边形ABCE是平行四边形。……………………………………………………6分
【3】 设OG=![]() ,则由折叠对称的性质,得GA=GC=8-
,则由折叠对称的性质,得GA=GC=8-![]() 。
。
在Rt△OAG中,由勾股定理,得![]() ,即
,即![]() ,
,
解得,![]() 。∴OG的长为1。………………………………………………………………10分
。∴OG的长为1。………………………………………………………………10分
【解析】
(1)由在△ABO中,∠OAB=90°,∠AOB=30°,OB=8,根据三角函数的知识,即可求得AB与OA的长,即可求得点B的坐标;
(2)首先可得CE∥AB,D是OB的中点,根据直角三角形斜边的中线等于斜边的一半,可证得BD=AD,∠ADB=60°,又由△OBC是等边三角形,可得∠ADB=∠OBC,根据内错角相等,两直线平行,可证得BC∥AE,继而可得四边形ABCD是平行四边形;
(3)首先设OG的长为x,由折叠的性质可得:AG=CG=8-x,然后根据勾股定理可得方程(8-x)2=x2+(4![]() )2,解此方程即可求得OG的长.
)2,解此方程即可求得OG的长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
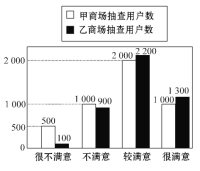
【题目】在“3·15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分.
(1)分别求出甲、乙两商场的用户满意度分数的平均值(计算结果精确到0.01).
(2)请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC如图(每个小正方形的边长均为1).

(1)请画出△ABC沿x轴向右平移4个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:A′(____,_____); B′(____,_____);C′(____,_____).
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制衣厂某车间计划用10天加工一批出口童装和成人装共360件,该车间的加工能力是:每天能单独加工童装45件或成人装30件。
(1)该车间应安排几天加工童装,几天加工成人装,才能如期完成任务?
(2)若加工童装一件可获利80元, 加工成人装一件可获利120元, 那么该车间加工完这批服装后,共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一股民在上星期五买进某公司股票1000股,每股27元,下表为本星期内每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股多少元?
星期三收盘时,每股多少元?
![]() 本星期内每股最低价多少元?
本星期内每股最低价多少元?
![]() 本周星期几抛售,获利最大,最大是多少?
本周星期几抛售,获利最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )
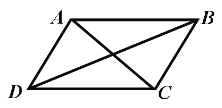
A. 当AC=BD时,四边形ABCD是矩形
B. 当AB=BC时,四边形ABCD是菱形
C. 当AC⊥BD时,四边形ABCD是菱形
D. 当∠DAB=90°时,四边形ABCD是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.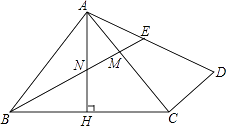
(1)若AB=3,AD= ![]() ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)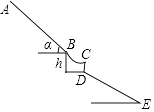
A.101.4
B.101.3
C.100.4
D.100.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
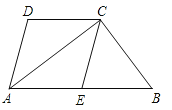
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com