
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.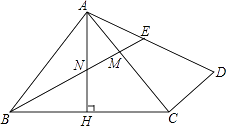
(1)若AB=3,AD= ![]() ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD= ![]() .
.
【答案】
(1)解:如图1中,
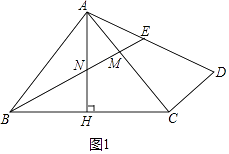
在△ABM和△CAD中,
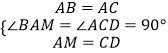 ,
,
∴△ABM≌△CAD,
∴BM=AD= ![]() ,
,
∴AM= ![]() =1,
=1,
∴CM=CA﹣AM=2,
∴S△BCM= ![]() CMBA=
CMBA= ![]() 23=3.
23=3.
(2)解:如图2中,连接EC、CN,作EQ⊥BC于Q,EP⊥BA于P.
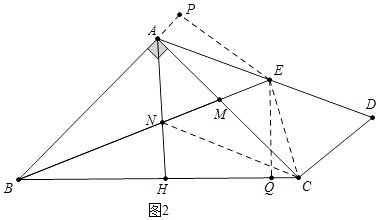
∵AE=ED,∠ACD=90°,
∴AE=CE=ED,
∴∠EAC=∠ECA,
∵△ABM≌△CAD,
∴∠ABM=∠CAD,
∴∠ABM=∠MCE,
∵∠AMB=∠EMC,
∴∠CEM=∠BAM=90°,
∵△ABM∽△ECM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠AME=∠BMC,
,∵∠AME=∠BMC,
∴△AME∽△BMC,
∴∠AEM=∠ACB=45°,
∴∠AEC=135°,易知∠PEQ=135°,
∴∠PEQ=∠AEC,
∴∠AEQ=∠EQC,∵∠P=∠EQC=90°,
∴△EPA≌△EQC,
∴EP=EQ,∵EP⊥BP,EQ⊥BC
∴BE平分∠ABC,
∴∠NBC=∠ABN=22.5°,
∵AH垂直平分BC,
∴NB=NC,
∴∠NCB=∠NBC=22.5°,
∴∠ENC=∠NBC+∠NCB=45°,
∴△ENC的等腰直角三角形,
∴NC= ![]() EC,∴AD=2EC,
EC,∴AD=2EC,
∴2NC= ![]() AD,
AD,
∴AD= ![]() NC,
NC,
∵BN=NC,
∴AD= ![]() BN.
BN.
【解析】(1)首先根据SAS证出△ABM≌△CAD,推出BM=AD= ![]() ,然后根据勾股定理得出AM的长,再推出CM=CA﹣AM=2,从而利用∴S△BCM=
,然后根据勾股定理得出AM的长,再推出CM=CA﹣AM=2,从而利用∴S△BCM= ![]() CMBA得出答案;
CMBA得出答案;
(2)如图2中,连接EC、CN,作EQ⊥BC于Q,EP⊥BA于P,想办法证出△ENC的等腰直角三角形,即可解决问题。
【考点精析】掌握线段垂直平分线的性质和勾股定理的概念是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
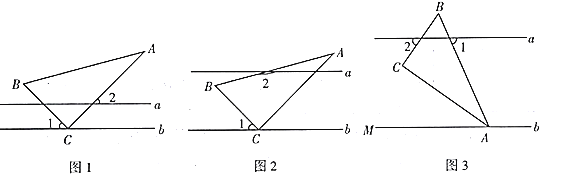
【题目】在综合与实践课上,同学们以“一个含![]() 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作发现:
(1)在如图1中,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,创新小组的同学把直线![]() 向上平移,并把
向上平移,并把![]() 的位置改变,发现
的位置改变,发现![]() ,说明理由;
,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,![]() 平分
平分![]() ,此时发现
,此时发现![]() 与
与![]() 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
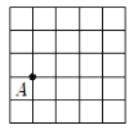
(1)已知点A在格点(即小正方形的顶点)上,画一条线段AB,长度为![]() ,且点B在格点上.
,且点B在格点上.
(2)以上题所画的线段AB为一边,另外两条边长分别为![]() ,
,![]() . 画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
. 画一个△ABC,使点C在格点上(只需画出符合条件的一个三角形).
(3)所画出的△ABC的边AB上的高线长为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△OAB中,∠OAB=90,∠AOB=30,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
【1】求点B的坐标
【2】求证:四边形ABCE是平行四边形;
【3】如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.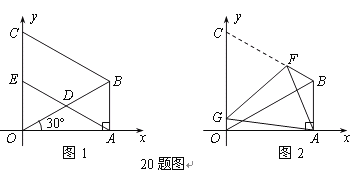
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
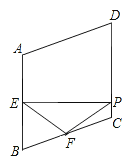
A. 35° B. 45° C. 50° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知线段![]() ,点C为线段AB上的一动点,点D、E分别是AC和BC中点.
,点C为线段AB上的一动点,点D、E分别是AC和BC中点.

![]() 若
若![]() ,求DE的长;
,求DE的长;
![]() 试说明无论AC取何值
试说明无论AC取何值![]() 不超过
不超过![]() ,DE的长不变;
,DE的长不变;
![]() 如图2,已知
如图2,已知![]() ,过角的内部一点C画射线OC,若OD、OE分别平分
,过角的内部一点C画射线OC,若OD、OE分别平分![]() 和
和![]() ,试说明
,试说明![]() 的度数与射线OC的位置无关.
的度数与射线OC的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
(1)若∠DBC=35°,则∠A的度数为________;
(2)若∠DBC=α,求∠A的度数(用含α的代数式表示);
(3)已知120°<∠ABC<180°,若点F在线段AE上,连接BF,当△BFD为直角三角形时,求∠A与∠FBE的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
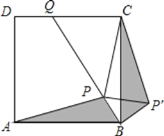
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为![]() ,1,2
,1,2![]() ,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com