
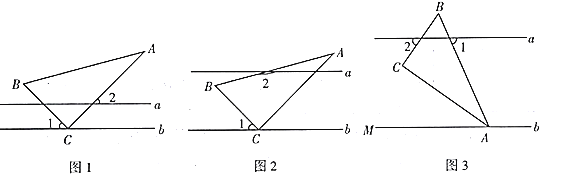
【题目】在综合与实践课上,同学们以“一个含![]() 的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线
的直角三角尺和两条平行线”为背景开展数学活动,如图,已知两直线![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
操作发现:
(1)在如图1中,![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,创新小组的同学把直线![]() 向上平移,并把
向上平移,并把![]() 的位置改变,发现
的位置改变,发现![]() ,说明理由;
,说明理由;
实践探究:
(3)缜密小组在创新小组发现结论的基础上,将如图中的图形继续变化得到如图,![]() 平分
平分![]() ,此时发现
,此时发现![]() 与
与![]() 又存在新的数量关系,请直接写出
又存在新的数量关系,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
【答案】操作发现:(1)![]() ;(2)见解析;实践探究:(3)
;(2)见解析;实践探究:(3)![]() .
.
【解析】
(1)如图1,根据平角定义先求出∠3的度数,再根据两直线平行,同位角相等即可得;
(2)如图2,过点B作BD//a,则有∠2+∠ABD=180°,根据已知条件可得∠ABD =60°-∠1,继而可得∠2+60°-∠1=180°,即可求得结论;
(3)∠1=∠2,如图3,过点C作CD//a,由已知可得∠CAM=∠BAC=30°,∠BAM=2∠BAC=60°,根据平行线的性质可得∠BCD=∠2,继而可求得∠1=∠BAM=60°,再根据∠BCD=∠BCA-∠DCA求得∠BCD=60°,即可求得∠1=∠2.
(1)如图1,
∵∠BCA=90°,∠1=46°,
∴∠3=180°-∠BCA-∠1=44°,
∵a//b,
∴∠2=∠3=44°;
(2)理由如下:如图2,过点B作BD//a,
∴∠2+∠ABD=180°,
∵a//b,
∴b//BD,
∴∠1=∠DBC,
∴∠ABD=∠ABC-∠DBC=60°-∠1,
∴∠2+60°-∠1=180°,
∴∠2-∠1=120°;
(3)∠1=∠2,理由如下:如图3,过点C作CD//a,
∵AC平分∠BAM,
∴∠CAM=∠BAC=30°,∠BAM=2∠BAC=2×30°=60°,
∵CD//a,
∴∠BCD=∠2,
∵a//b,
∴∠1=∠BAM=60°,b//CD,
∴∠DCA=∠CAM=30°,
∵∠BCD=∠BCA-∠DCA,
∴∠BCD=90°-30°=60°,
∴∠2=60°,
∴∠1=∠2.


科目:初中数学 来源: 题型:
【题目】在抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从![]() 地出发,晚上到达
地出发,晚上到达![]() 地,约定向东为正方向,当天的航行路程记录如下(单位:千米):
地,约定向东为正方向,当天的航行路程记录如下(单位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)请你帮忙确定![]() 地位于
地位于![]() 地的什么方向,距离
地的什么方向,距离![]() 地多少千米?
地多少千米?
(2)若冲锋舟每千米耗油![]() 升,邮箱容量为
升,邮箱容量为![]() 升,求冲锋舟当天救灾过程中至少还需补充多少升油?
升,求冲锋舟当天救灾过程中至少还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家住房的地面结构如图所示,请根据图中的数据,解答下列问题:
(1)用含x的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多![]() 这家房子的主人打算把厨房和卫生间都铺上地砖,已知铺
这家房子的主人打算把厨房和卫生间都铺上地砖,已知铺![]() 地砖的平均费用为60元,求铺地砖的总费用为多少元?
地砖的平均费用为60元,求铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
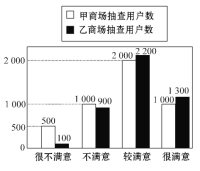
【题目】在“3·15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分.
(1)分别求出甲、乙两商场的用户满意度分数的平均值(计算结果精确到0.01).
(2)请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读并回答:
科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线![]() 与
与![]() 射向一个水平镜面后被反射,此时
射向一个水平镜面后被反射,此时![]() ,
,![]() .
.
①由条件可知:![]() 与
与![]() 的大小关系是____________,理由是____________;
的大小关系是____________,理由是____________;![]() 与
与![]() 的大小关系是____________;
的大小关系是____________;
②反射光线![]() 与
与![]() 的位置关系是____________,理由是____________;
的位置关系是____________,理由是____________;
(2)解决问题:
如图2,,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 镜反射,若
镜反射,若![]() 反射出的光线
反射出的光线![]() 平行于
平行于![]() ,且
,且![]() ,求
,求![]() 和
和![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
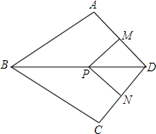
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC如图(每个小正方形的边长均为1).

(1)请画出△ABC沿x轴向右平移4个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:A′(____,_____); B′(____,_____);C′(____,_____).
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.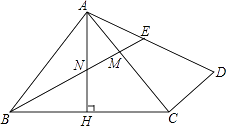
(1)若AB=3,AD= ![]() ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com