【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分ABC，P是BD上一点，过点P作PM^AD，PN^CD，垂足分别为M、N。
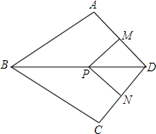
（1）求证：ADB=CDB；
（2）若ADC=90°，求证：四边形MPND是正方形。
【答案】见解析
【解析】
试题（1）根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD，由全等三角形的性质即可得到：∠ADB=∠CDB；
（2）若∠ADC=90°，由（1）中的条件可得四边形MPND是矩形，再根据两边相等的四边形是正方形即可证明四边形MPND是正方形．
证明：（1）∵对角线BD平分∠ABC，
∴∠ABD=∠CBD，
在△ABD和△CBD中，
，
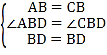∴△ABD≌△CBD（SAS），
∴∠ADB=∠CDB；
（2）∵PM⊥AD，PN⊥CD，
∴∠PMD=∠PND=90°，
∵∠ADC=90°，
∴四边形MPND是矩形，
∵∠ADB=∠CDB，
∴∠ADB=45°
∴PM=MD，
∴四边形MPND是正方形．
口算题卡北京妇女儿童出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．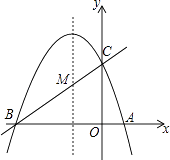
（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；
（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；
（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据题意结合图形填空：如图，
点
在
上，点
在
上，
，
.试说明：∥.将过程补充完整.
解：∵（已知）
且
（ ）
∴
（等量代换）
∴ ∥ （ ）
∴
（ ）
又∵（已知）
∴ = （等量代换 ）
∴∥（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
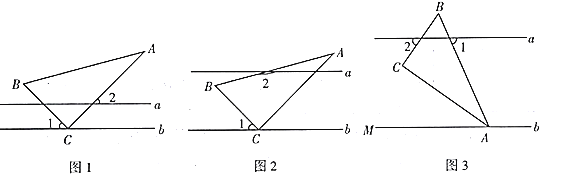
【题目】在综合与实践课上，同学们以“一个含
的直角三角尺和两条平行线”为背景开展数学活动，如图，已知两直线
且
和直角三角形
，
，
，
.
操作发现：
（1）在如图1中，
，求
的度数；
（2）如图2，创新小组的同学把直线
向上平移，并把的位置改变，发现
，说明理由；
实践探究：
（3）缜密小组在创新小组发现结论的基础上，将如图中的图形继续变化得到如图，
平分
，此时发现
与又存在新的数量关系，请直接写出与的数量关系.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“PM2.5”指数是空气中可入肺颗粒物的含量，是空气质量的指标之一．下表为A市1﹣12月“PM2.5月平均指数”（单位：微克/立方米）
PM2.5指数 | 20 | 30 | 40 | 41 | 43 | 50 |
月数 | 2 | 4 | 3 | 1 | 1 | 1 |
（1）求这12个月“PM2.5月平均指数”的众数、中位数、平均数；
（2）根据《环境空气质量标准》，宜居城市的标准之一是“PM2.5年平均指数少于35微克/立方米”，请你判断A市是否为宜居城市？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在安庆市第三届中小学生道路交通安全网络知识竞赛活动中，某中学的老师要求同学们都参加社会实践活动，一天，王明和张强两位同学到市中心的广场的十字路口，观察、统计上午7：
：00中闯红灯的人次，制作了如下的两个数据统计图
井且提出了一些问题
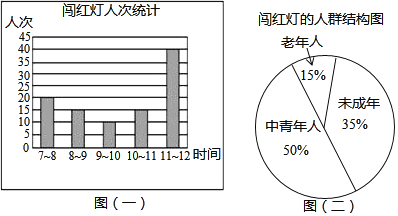
求图
一
提供的五个数据各时段闯红灯人次的平均数并说明这两幅统计图各有什么特点？
估计一个月按30天计算上午7：：00在该十字路口闯红灯的未成年人约有多少人次？
请你根据统计图提供的信息向交通管理部门提出一条合理化建议．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“一带一路”国际合作高峰论坛于5月14日在北京开幕，学校在初三年级随机抽取了50名同学进行“一带一路”知识竞答，并将他们的竞答成绩绘制成如图的条形统计图，本次知识竞答成绩的中位数是分．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在5×5的正方形网格中，每个小正方形的边长为1，请在所给网格中按下列要求画出图形.
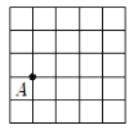
（1）已知点A在格点（即小正方形的顶点）上，画一条线段AB，长度为
，且点B在格点上.
（2）以上题所画的线段AB为一边，另外两条边长分别为
，
. 画一个△ABC，使点C在格点上（只需画出符合条件的一个三角形）.
（3）所画出的△ABC的边AB上的高线长为 .（直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD∥BC，BE平分∠ABC交AD于点E，BD平分∠EBC．
（1）若∠DBC=35°，则∠A的度数为________；
（2）若∠DBC=α，求∠A的度数（用含α的代数式表示）；
（3）已知120°<∠ABC<180°，若点F在线段AE上，连接BF，当△BFD为直角三角形时，求∠A与∠FBE的数量关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com