
【题目】如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC.
(1)若∠DBC=35°,则∠A的度数为________;
(2)若∠DBC=α,求∠A的度数(用含α的代数式表示);
(3)已知120°<∠ABC<180°,若点F在线段AE上,连接BF,当△BFD为直角三角形时,求∠A与∠FBE的数量关系.

【答案】(1)40°;(2)∠A=180°-4α;(3)∠A=4∠FBE-180°或∠A=2∠FBE.
【解析】
(1)根据角平分线的定义分别求出∠EBC和∠ABC,然后利用平行线的性质求∠A即可;
(2)根据角平分线的定义分别表示出∠EBC和∠ABC,然后利用平行线的性质求∠A即可;
(3)分两种情况讨论:①当∠FBD=90°时,②当∠BFD=90°时,分别用∠FBE表示出∠A即可.
解:(1)因为BD平分∠EBC,∠DBC=35°,
所以∠EBC=2∠DBC=70°,
因为BE平分∠ABC,
所以∠ABC=2∠EBC =140°,
因为AD∥BC,
所以∠A+∠ABC=180°.
所以∠A=40°;
(2)因为BD平分∠EBC,∠DBC=α,
所以∠EBC=2∠DBC=2α.
因为BE平分∠ABC,
所以∠ABC=4α,
因为AD∥BC,
所以∠A+∠ABC=180°,
所以∠A=180°-4α;
(3)设∠DBC=α,由(2)可知:∠A=180°-4α,∠EBC=2α,
①当∠FBD=90°时,∠FBE+∠EBD=90°,
所以∠FBE=90°-∠EBD=90°-α,
所以α=90°-∠FBE,
所以∠A=180°-4(90°-∠FBE)=4∠FBE-180°;
②当∠BFD=90°时,
因为AD∥BC,
所以∠FBC=180°-∠BFD=90°,∠FBE+∠EBC=90°,
所以∠FBE=90°-∠EBC=90°-2α,
所以2α=90°-∠FBE,
所以∠A=180°-2(90°-∠FBE)=2∠FBE,
综上所述:∠A=4∠FBE-180°或∠A=2∠FBE.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
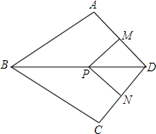
(1)求证:ADB=CDB;
(2)若ADC=90°,求证:四边形MPND是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一股民在上星期五买进某公司股票1000股,每股27元,下表为本星期内每日该股票的涨跌情况![]() 单位:元
单位:元![]()
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股多少元?
星期三收盘时,每股多少元?
![]() 本星期内每股最低价多少元?
本星期内每股最低价多少元?
![]() 本周星期几抛售,获利最大,最大是多少?
本周星期几抛售,获利最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.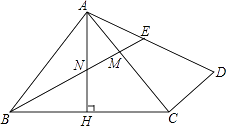
(1)若AB=3,AD= ![]() ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数 ![]() (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 ![]() 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)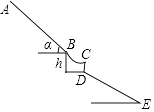
A.101.4
B.101.3
C.100.4
D.100.3
查看答案和解析>>
科目:初中数学 来源: 题型:
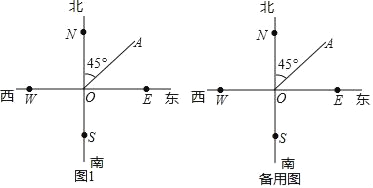
【题目】如图,射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向,点A在点O的北偏东45°方向,点B在点O的北偏西30°方向.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图1或备用图中画出∠BOC;
(2)若OP是∠AOC的角平分线,直接写出∠AOP的度数(不需要计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.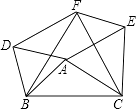
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对我校七年级(1)班喜欢什么球类运动的调查,下列图形中的左图是小明对所调查结果的条形统计图.

(1)问七年级(1)班共有多少学生?
(2)请你改用扇形统计图来表示我校七年级(1)班同学喜欢的球类运动.
(3)从统计图中你可以获得哪些信息?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com