
【题目】某农业观光园将一块面积为![]() 的观光园分成
的观光园分成![]() 三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲
三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株.已知
株.已知![]() 区域的面积是
区域的面积是![]() 的
的![]() 倍,记A区域的面积为
倍,记A区域的面积为![]() 区域的面积为
区域的面积为![]() .
.
花卉 项目 | 甲 | 乙 | 丙 |
面积 |
|
| |
株/ |
|
|
|
数量 |
|
(1)完成上表(结果用含![]() 的代数式表示).
的代数式表示).
(2)若三种花卉共栽种![]() 株
株
①求![]() 与
与![]() 的值.
的值.
②若三种花卉的单价(都是整数)之和为![]() 元,全部栽种共需
元,全部栽种共需![]() 元,求种植面积最大的花卉总价.
元,求种植面积最大的花卉总价.
【答案】(1)见解析;(2)①![]() ,
,![]() ;②11200或5600元
;②11200或5600元
【解析】
(1)记A区域面积为x,则B区域面积是2x,根据每平方米栽种甲2株或乙4株,即可解答;
(2)①根据![]() 三个区域的总面积为
三个区域的总面积为![]() ,三种花卉共栽种
,三种花卉共栽种![]() 株,列二元一次方程组求解即可;
株,列二元一次方程组求解即可;
②设三种花卉的单价分别为a元、b元、c元,根据三种花卉的单价(都是整数)之和为![]() 元,全部栽种共需
元,全部栽种共需![]() 元,列出三元一次方程组,分析求解即可.
元,列出三元一次方程组,分析求解即可.
(1) 记A区域面积为x,则B区域面积是2x,
∵甲、乙、丙三种花卉,每平方米栽种甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株,
株,
∴甲花卉种植数量:2x,乙花卉种植数量:8x;
表如下:
花卉 项目 | 甲 | 乙 | 丙 |
面积 |
| 2x |
|
株/ |
|
|
|
数量 | 2x | 8x |
|
(2) ①根据题意列方程组:![]()
解方程组得:![]() ,
,
∴![]() ,
,![]() ;
;
②设三种花卉的单价分别为a元、b元、c元,
由(2)可知,分别种植甲、乙、丙三种花卉的株数为280株,1120株,1680株,
根据题意得:![]() ,
,
整理得:3b+5c=35,
∴b=10,c=1或b=5,c=4,
∵三种花卉的单价(都是整数)之和为40元,
∴a=29或a=31,
∴a=29,b=10,c=1或a=31,b=5,c=4,
由(2)可知乙种花卉种植280亩,面积最大,
∴种植面积最大的花卉总价为:280×4×10=11200(元)或280×4×5=5600(元)
答:种植面积最大的花卉总价为11200或5600元.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
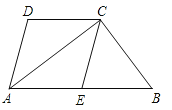
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明一家到某拓展基地训练,![]() 小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发
小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发![]() 他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地
他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地![]() 如图是他们离家的距离s
如图是他们离家的距离s![]() km
km![]() 与小明离家的时问t
与小明离家的时问t![]() 的关系图.
的关系图.
(1)请根据图象,回答问题:
①图中点A表示的意义是 .
②当爸爸第一次到达度假村后,小明离度假村的距离是______ km;
(2)爸爸在返回家的途中与小明相遇时,小明离家的距离是多少?
(3)整个运动过程中(双方全部到达会合时,视为运动结束),请直接写出小明与爸爸相距24km时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB、CD相交于点O,OE平分∠BOD.OF⊥CD,垂足为O,若∠EOF=54°.
(1)求∠AOC的度数;
(2)作射线OG⊥OE,试求出∠AOG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
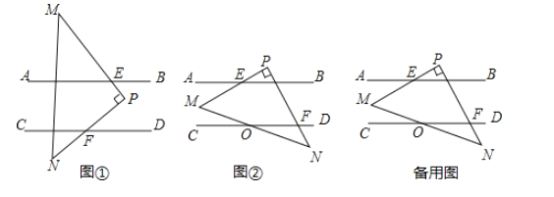
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]()
(1)当![]() 所放位置如图①所示时,则
所放位置如图①所示时,则![]() 与
与![]() 的数量关系为_______;请说明理由.
的数量关系为_______;请说明理由.
(2)当![]() 所放位置如图②所示时,
所放位置如图②所示时,![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(3)在(2)的条件下,若![]() 与
与![]() 交于点0,且
交于点0,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
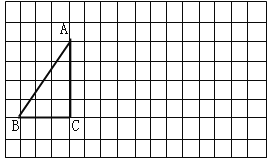
【题目】将下列方格纸中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)画出平移后的三角形;
.(1)画出平移后的三角形;
(2)若AB=5,则![]() = .
= .
(3)连接AA1,BB1, 根据“图形平移”的性质,得:线段AA1与线段BB1的数量关系和位置关系是: .
(4)求图中∠![]() AC+∠
AC+∠![]() BC的度数.
BC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,又
,又![]() ,
,
![]() ,∴能确定59319的立方根是个两位数.
,∴能确定59319的立方根是个两位数.
②∵59319的个位数是9,又![]() ,∴能确定59319的立方根的个位数是9.
,∴能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数195112,按这种方法求立方根,请完成下列填空.
①它的立方根是_______位数.
②它的立方根的个位数是_______.
③它的立方根的十位数是__________.
④195112的立方根是________.
(2)请直接填写结果:
①![]() ________.
________.
②![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.
(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
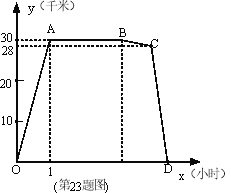
【题目】(2011福建龙岩,23, 12分) 周六上午8:00小明从家出发,乘车1小时到郊外某基地参加社会实践活动,在基地活动2.2小时后,因家里有急事,他立即按原路以4千米/时的平均速度步行返回.同时爸爸开车从家出发沿同一路线接他,在离家28千米处与小明相遇。接到小明后保持车速不变,立即按原路返回.设小明离开家的时间为x小时,小名离家的路程y (干米) 与x (小时)之间的函致图象如图所示,
(1)小明去基地乘车的平均速度是________千米/小时,爸爸开车的平均速度应是________千米/小时;
(2)求线段CD所表示的函敛关系式;
(3)问小明能否在12:0 0前回到家?若能,请说明理由:若不能,请算出12:00时他离家的路程,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com