
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]()
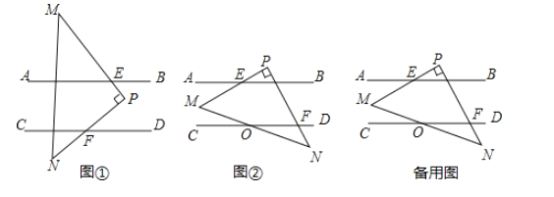
(1)当![]() 所放位置如图①所示时,则
所放位置如图①所示时,则![]() 与
与![]() 的数量关系为_______;请说明理由.
的数量关系为_______;请说明理由.
(2)当![]() 所放位置如图②所示时,
所放位置如图②所示时,![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(3)在(2)的条件下,若![]() 与
与![]() 交于点0,且
交于点0,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)![]() ;理由见解析;(2)
;理由见解析;(2)![]() ;(3)∠N=45°.
;(3)∠N=45°.
【解析】
(1)如下图,作PH∥AB,利用AB∥HP,HP∥CD转化角度可得;
(2)∠PFD和∠PFO互补,将∠PFO转化为∠FON和∠FNO,结合第一问的结论可得;
(3)利用第二问的结论,直接代入计算即可
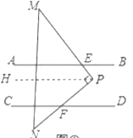
解:(1)关系:![]()
理由:如下图,作![]()
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)关系:![]()
如下图,作MG∥AB交PN于点G
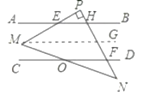
同上,∠PMN=∠AEM+∠MOC
∵∠PFC=∠FON+∠FNO
∴∠PFC=∠MOC+∠FNO
∴∠AEM+∠PFD=∠AEM+∠MOC+∠PNO=∠PMN+∠PNO
∵∠P=90°
∴∠AEM+∠PFC=∠PMN+∠PNO=90°
∠PFC=180°-∠PFD代入得:∠AEM+180°-∠PFD=90°
化简得:∠PFD-∠AEM=90°
(3)由(2)得,![]() ,
,
![]()
![]()


科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() .
.![]() 这两直线之间一点.
这两直线之间一点.
(1)如图1,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.

(2)如图2,若![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并证明你的结论.
有何数量关系?并证明你的结论.
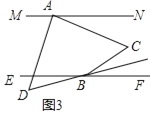
(3)如图3,若![]() 的平分线与
的平分线与![]() 的平分线所在的直线相交于点
的平分线所在的直线相交于点![]() ,请直接写出
,请直接写出![]() 与
与![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
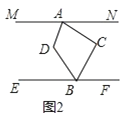
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.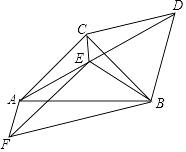
(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A表示的数为![]() ,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动
,点B表示的数为16,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动![]() 设运动时间为t秒
设运动时间为t秒![]() .
.
![]() ,B两点间的距离等于______,线段AB的中点表示的数为______;
,B两点间的距离等于______,线段AB的中点表示的数为______;
![]() 用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______;
用含t的代数式表示:t秒后,点P表示的数为______,点Q表示的数为______;
![]() 求当t为何值时,
求当t为何值时,![]() ?
?
![]() 若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变请直接写出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农业观光园将一块面积为![]() 的观光园分成
的观光园分成![]() 三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲
三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株.已知
株.已知![]() 区域的面积是
区域的面积是![]() 的
的![]() 倍,记A区域的面积为
倍,记A区域的面积为![]() 区域的面积为
区域的面积为![]() .
.
花卉 项目 | 甲 | 乙 | 丙 |
面积 |
|
| |
株/ |
|
|
|
数量 |
|
(1)完成上表(结果用含![]() 的代数式表示).
的代数式表示).
(2)若三种花卉共栽种![]() 株
株
①求![]() 与
与![]() 的值.
的值.
②若三种花卉的单价(都是整数)之和为![]() 元,全部栽种共需
元,全部栽种共需![]() 元,求种植面积最大的花卉总价.
元,求种植面积最大的花卉总价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的弦,半径OA=2cm,∠AOB=120°
(1)求tan∠OAB的值;
(2)求图中阴影部分的面积S;
(3)在⊙O上一点P从A点出发,沿逆时针方向运动一周,回到点A,在点P的运动过程中,满足S△POA=S△AOB时,直接写出P点所经过的弧长(不考虑点P与点B重合的情形).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从社会效益和经济效益出发,某地制定了三年规划,投入资金进行生态环境建设,并以此发展旅游产业。根据规划,第一年度投入资金800万元,第二年度比第一年度减少![]() ,第三年度比第二年度减少
,第三年度比第二年度减少![]() 。第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,旅游业收入的年增长率应是多少?(以下数据供选用:
。第一年度当地旅游业收入估计为400万元,要使三年内的投入资金与旅游业总收入持平,旅游业收入的年增长率应是多少?(以下数据供选用: ![]() =1.414,
=1.414, ![]() =3.606 计算结果精确到百分位)
=3.606 计算结果精确到百分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从相距30千米的A、B两地同时相向而行,经过3小时后相距3千米,再经过2小时,甲到B地所剩的路程是乙到A地所剩路程的2倍,试求甲、乙两人的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com