
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.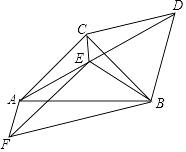
(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
【答案】
(1)解:延长CE交AB于G,
∵△BAC是等腰直角三角形,CE平分∠ACB,
∴CG⊥AB,
∴∠AGC=90°,
∵CA=CB,∠ACB=90°,
∴∠CAB=45°,
∴△CAG是等腰直角三角形,
∵△BCD是等边三角形,
∴BC=CD=AC,∠BCD=60°,
∴∠CAD=∠CDA,
∴∠ACD=∠ACB+∠BCD=150°,
∴∠CAD=∠CDA=15°,
∴∠EAB=∠CAB﹣∠CAD=30°,
在Rt△AEG中,∠EAG=30°,AE=2,
∴AE= ![]() ,EG=1,
,EG=1,
∵CG=AG= ![]() ,
,
∴CE=CG﹣EG= ![]() ﹣1.
﹣1.
(2)解:延长FB到H,使得BH=AF,连接EH.作EI⊥BF于I.
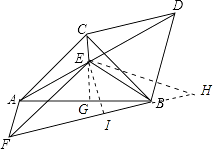
由(1)可知:AC=BC,CE平分∠ACB,
∴∠ACE=∠BCE,
∵CE=CE,
∴△ACE≌△BCE,
∴AE=BE,
∴∠EAB=∠EBC=30°,
在△AFB中,∠AFB=60°,
∴∠FAB+∠FBA=120°,
∴∠FAE=∠EAB+∠FAB=30°+∠FAB,
∠EBH=180°﹣∠EBA﹣∠ABF=150°﹣(120°﹣∠ABF)=30°+∠FAB,
∴∠EBH=∠FAE,
∴△AFE≌△BHE,
∴∠AFE=∠BHE,EF=EH,
∴∠EFB=∠EBH=∠AFE=30°,
∵EI⊥FH,
∴EI=IH,
在Rt△FEI中,∠EFI=30°,
∴FI= ![]() FE,
FE,
∴FH=BH+FB= ![]() FE,
FE,
∴FA+FB= ![]() FE.
FE.
【解析】(1)延长CE交AB于G,首先判断出△CAG是等腰直角三角形,然后找到∠EAB=∠CAB﹣∠CAD=30°,分别求出CG,EG即可解决问题;
(2)延长FB到H,使得BH=AF,连接EH.作EI⊥BF于I.由△ACE≌△BCE,推出AE=BE,推出∠EAB=∠EBC=30°,由△AFE≌△BHE,推出∠AFE=∠BHE,EF=EH,可得∠EFB=∠EBH=∠AFE=30°,又EI⊥FH,故在Rt△FEI中,∠EFI=30°,从而得出FI= ![]() FE,可得FA+FB=
FE,可得FA+FB= ![]() FE.
FE.
【考点精析】本题主要考查了等腰直角三角形和等边三角形的性质的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
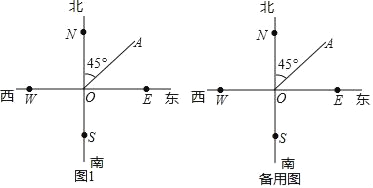
【题目】如图,射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向,点A在点O的北偏东45°方向,点B在点O的北偏西30°方向.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图1或备用图中画出∠BOC;
(2)若OP是∠AOC的角平分线,直接写出∠AOP的度数(不需要计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为BC上一点,BE=2CE,连接DE,F为DE中点,以DF为直角边作等腰Rt△DFG,连接BG,将△DFG绕点D顺时针旋转得△DF′G′,G′恰好落在BG的延长线上,连接F′G,若BG=2 ![]() ,则S△GF′G′= .
,则S△GF′G′= . 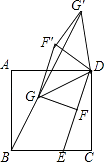
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对我校七年级(1)班喜欢什么球类运动的调查,下列图形中的左图是小明对所调查结果的条形统计图.

(1)问七年级(1)班共有多少学生?
(2)请你改用扇形统计图来表示我校七年级(1)班同学喜欢的球类运动.
(3)从统计图中你可以获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24 ㎝,BC=26㎝,动点P从点A开始沿AD边以每秒1㎝的速度向D点运动,动点Q从点C开始沿CB边以每秒3㎝的速度向B运动,P,Q分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t s.
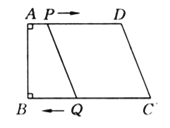
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?
(3)t为何值时,四边形ABQP为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明一家到某拓展基地训练,![]() 小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发
小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发![]() 他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地
他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地![]() 如图是他们离家的距离s
如图是他们离家的距离s![]() km
km![]() 与小明离家的时问t
与小明离家的时问t![]() 的关系图.
的关系图.
(1)请根据图象,回答问题:
①图中点A表示的意义是 .
②当爸爸第一次到达度假村后,小明离度假村的距离是______ km;
(2)爸爸在返回家的途中与小明相遇时,小明离家的距离是多少?
(3)整个运动过程中(双方全部到达会合时,视为运动结束),请直接写出小明与爸爸相距24km时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,圆的周长为4个单位长度在圆周的4等分点处标上字母A,B,C,D,先将圆周上的字母A对应的点与数轴上的原点重合,再将圆沿着数轴向右滚动,那么数轴上的1949所对应的点与圆周上字母![]()
![]() 所对应的点重合.
所对应的点重合.
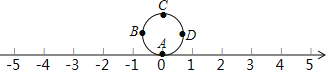
A. AB. BC. CD. D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,现将一直角三角形
,现将一直角三角形![]() 放入图中,其中
放入图中,其中![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]()
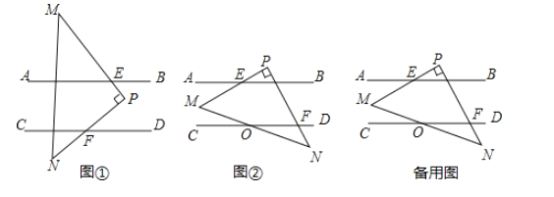
(1)当![]() 所放位置如图①所示时,则
所放位置如图①所示时,则![]() 与
与![]() 的数量关系为_______;请说明理由.
的数量关系为_______;请说明理由.
(2)当![]() 所放位置如图②所示时,
所放位置如图②所示时,![]() 与
与![]() 的数量关系为________;
的数量关系为________;
(3)在(2)的条件下,若![]() 与
与![]() 交于点0,且
交于点0,且![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校. 图中的折线表示清清的行程s(米)与所花时间t (分)之间的函数关系. 下列说法错误的是( )

A. 清清等公交车时间为3分钟 B. 清清步行的速度是80米/分
C. 公交车的速度是500米/分 D. 清清全程的平均速度为290米/分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com