
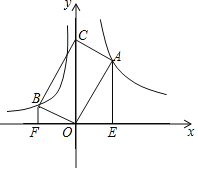
【题目】如图,点A、B在x轴的上方,∠AOB=90°,OA、OB分别与函数![]() 、
、![]() 的图象交于A、B两点,以OA、OB为邻边作矩形AOBC.当点C在y轴上时,分别过点A和点B作AE⊥x轴,BF⊥x轴,垂足分别为E、F,则
的图象交于A、B两点,以OA、OB为邻边作矩形AOBC.当点C在y轴上时,分别过点A和点B作AE⊥x轴,BF⊥x轴,垂足分别为E、F,则![]() =_______.
=_______.
科目:初中数学 来源: 题型:
【题目】今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1000米,斜坡BC的长为200![]() 米,在C点测得B点的俯角为45°,已知A点海拔21米,C点海拔721米.
米,在C点测得B点的俯角为45°,已知A点海拔21米,C点海拔721米.
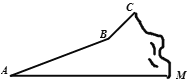
(1)求B点的海拔;
(2)求斜坡AB的坡角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.
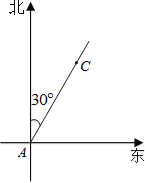
(1)请在图中作出该船在点B处的位置;
(2)求钓鱼岛C到B处距离(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=﹣1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标;
(2)求二次函数的解析式;
(3)已知C为抛物线与y轴的交点,设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
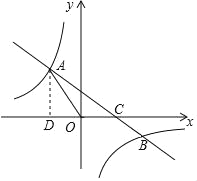
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点,与x轴交于点C,点B 坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)点E是x轴上一点,且△AOE是等腰三角形,请直接写出所有符合条件的E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
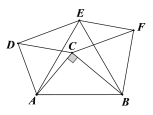
【题目】如图,△ACB中,∠ACB=90°,在AB的同侧分别作正△ACD、正△ABE和正△BCF. 若四边形CDEF的周长是24,面积是17,则AB的长是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(1,5),直线l1:y=x,直线l2过原点且与x轴正半轴成60°夹角,在l1上有一动点M,在l2上有一动点N,连接AM、MN,则AM+MN的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚C处测得一座建筑物定点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=60m,山坡的坡比为1:2.
(1)求该建筑物的高度(即AB的长,结果保留根号);
(2)求此人所在位置点P的铅直高度(即PD的长,结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
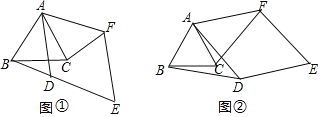
【题目】已知△ABC是等边三角形,四边形ADEF是菱形,∠ADE=120°(AD>AB).
(1)如图①,当AD与边BC相交,点D与点F在直线AC的两侧时,BD与CF的数量关系为___________.
(2)将图①中的菱形ADEF绕点A在平面内逆时针旋转α(0°<α<180°).
Ⅰ.判断(1)中的结论是否仍然成立,请利用图②证明你的结论.
Ⅱ.若AC=4,AD=6,当△ACE为直角三角形时,直接写出CE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com